Lab 4

Author

Filippo Gambarota 

devtools::load_all() # if using the rproject dowloaded from the slides
# source("utils-glm.R") # if using a standard setup
library(here)
library(tidyr) # for data manipulation
library(dplyr) # for data manipulation
library(ggplot2) # plotting
library(car) # general utilities
library(effects) # for extracting and plotting effects 
library(emmeans) # for marginal means
data("tantrums")
dat <- tantrums

Overview

The dataset tantrums.csv is about the number of tantrums of nrow(child) toddlers during two days at the nursery. The columns are:

  • id: identifier for the child
  • temperament: the temperament of the child as “easy” or “difficult”
  • attachment: the attachment of the child as “secure” or “insecure”
  • parent_se: an average self-esteem value of the parents (self report)
  • parent_skills: a score representing the teacher judgment about parenting skills
  • tantrums: the number of tantrums

We want to predict the number of tantrums as a function of these predictors.

  1. Importing data and check
    • in the presence of NA, remove the children
    • convert to factors the categorical variable with “difficult” and “insecure” as reference values
  2. Exploratory data analysis
  3. Model fitting with glm()
  4. Diagnostic
  5. Interpreting parameters
  6. Model selection
  7. What about interactions?

1. Importing data and check

Check the structure:

str(dat)
'data.frame':   122 obs. of  6 variables:
 $ id           : int  1 2 3 4 5 6 7 8 9 10 ...
 $ temperament  : chr  "difficult" "easy" "difficult" "difficult" ...
 $ attachment   : chr  "insecure" "secure" "secure" "secure" ...
 $ parent_se    : int  3 4 9 8 4 6 10 6 10 4 ...
 $ parent_skills: int  5 8 5 6 7 2 9 7 1 7 ...
 $ tantrum      : int  1 0 1 0 0 10 0 2 7 0 ...

Check for NA:

sapply(dat, function(x) sum(is.na(x)))
           id   temperament    attachment     parent_se parent_skills 
            0             1             1             0             0 
      tantrum 
            2

So we have some NA values. We managed them according to the instructions:

dat <- dat[complete.cases(dat), ]
dat$id <- 1:nrow(dat) # restore the id
rownames(dat) <- NULL

Let’s convert the categorical variables into factor with the appropriate reference level:

dat$temperament <- factor(dat$temperament, levels = c("difficult", "easy"))
dat$temperament[1:5]
[1] difficult easy      difficult difficult difficult
Levels: difficult easy
dat$attachment <- factor(dat$attachment, levels = c("insecure", "secure"))
dat$attachment[1:5]
[1] insecure secure   secure   secure   insecure
Levels: insecure secure

2. Exploratory data analysis

Let’s compute some summary statistics and plots.

summary(dat)
       id            temperament    attachment   parent_se     
 Min.   :  1.00   difficult:32   insecure:39   Min.   : 1.000  
 1st Qu.: 30.25   easy     :86   secure  :79   1st Qu.: 5.000  
 Median : 59.50                                Median : 7.000  
 Mean   : 59.50                                Mean   : 6.364  
 3rd Qu.: 88.75                                3rd Qu.: 8.000  
 Max.   :118.00                                Max.   :10.000  
 parent_skills       tantrum     
 Min.   : 1.000   Min.   : 0.00  
 1st Qu.: 5.000   1st Qu.: 0.00  
 Median : 6.000   Median : 1.00  
 Mean   : 6.237   Mean   : 1.72  
 3rd Qu.: 8.000   3rd Qu.: 2.00  
 Max.   :10.000   Max.   :20.00  
table(dat$temperament)

difficult      easy 
       32        86 
table(dat$attachment)

insecure   secure 
      39       79 
table(dat$attachment, dat$temperament)
          
           difficult easy
  insecure        12   27
  secure          20   59
par(mfrow = c(1,3))
hist(dat$parent_se)
hist(dat$parent_skills)
hist(dat$tantrum)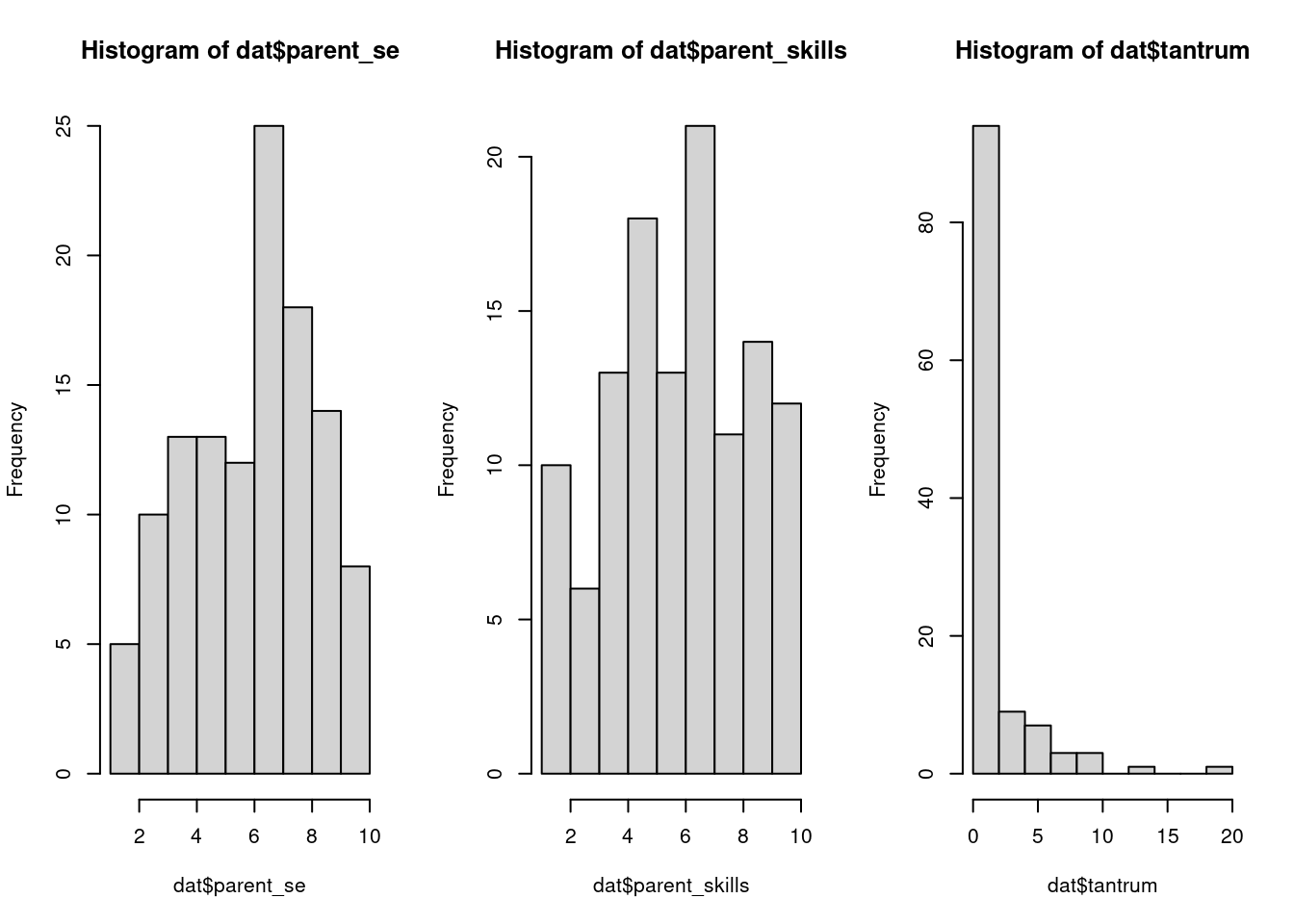

Let’s compute some bivariate relationships:

plot(dat$parent_se, dat$tantrum, pch = 19)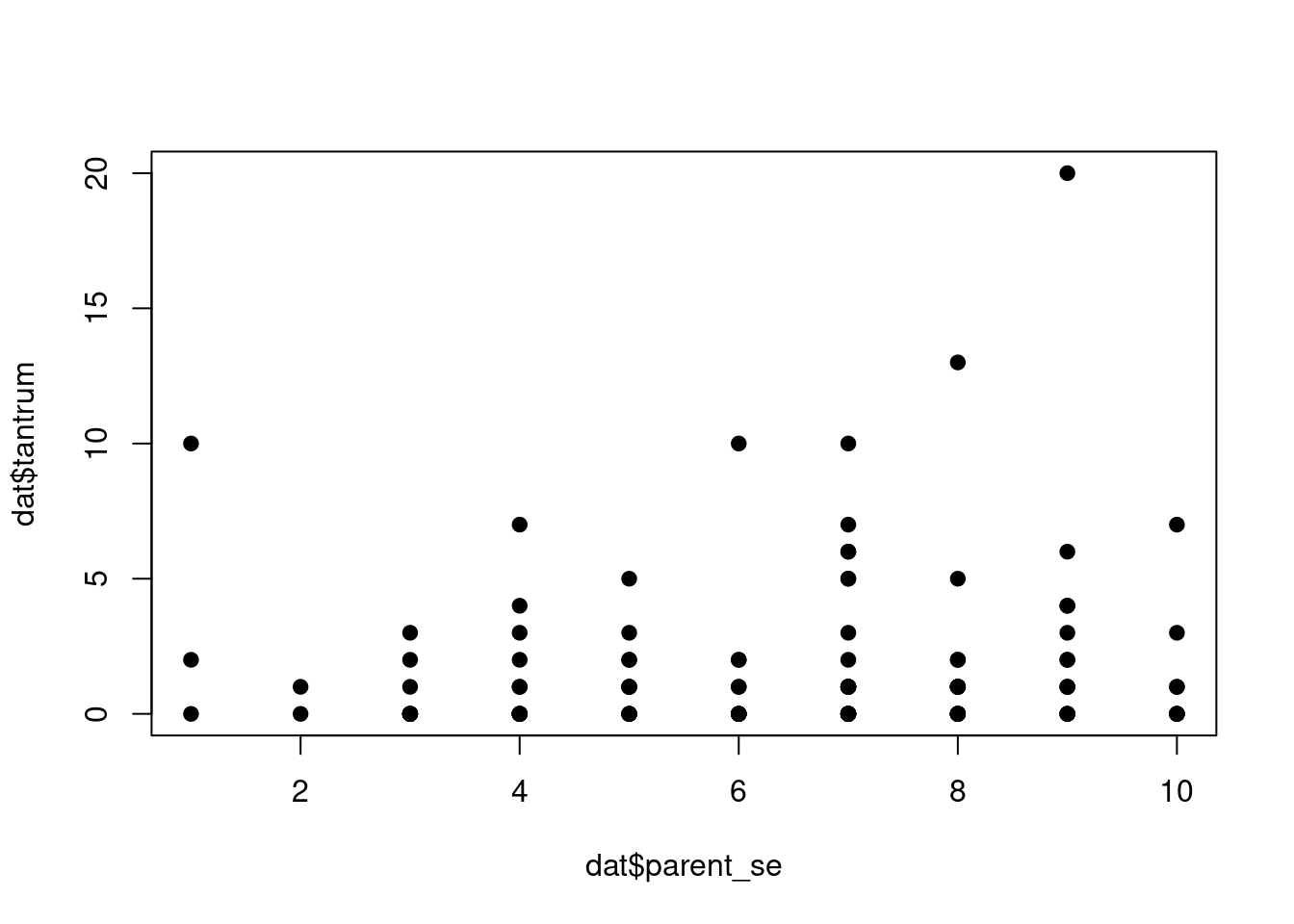

plot(dat$parent_skills, dat$tantrum, pch = 19)

boxplot(tantrum ~ temperament, data = dat)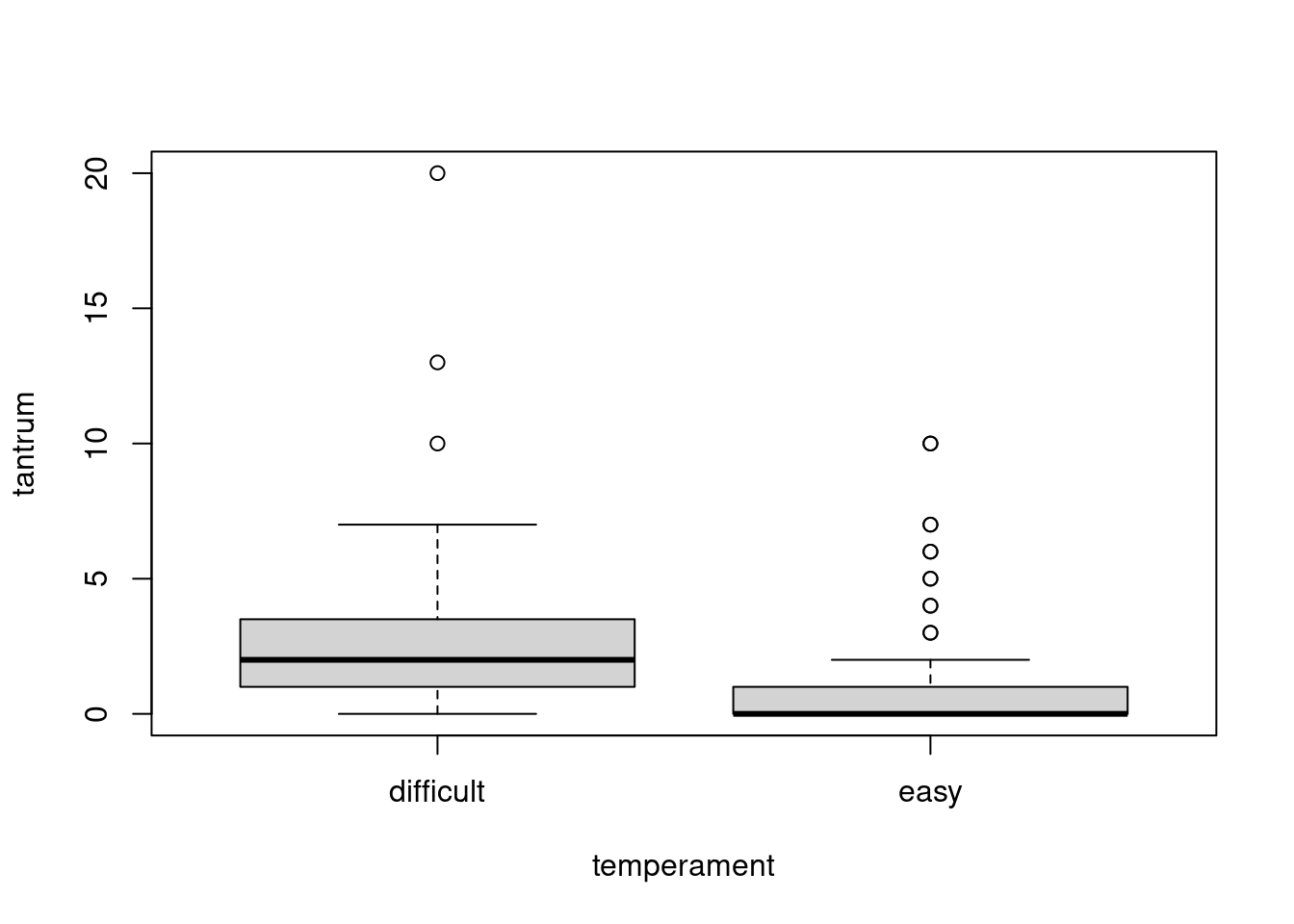

boxplot(tantrum ~ attachment, data = dat)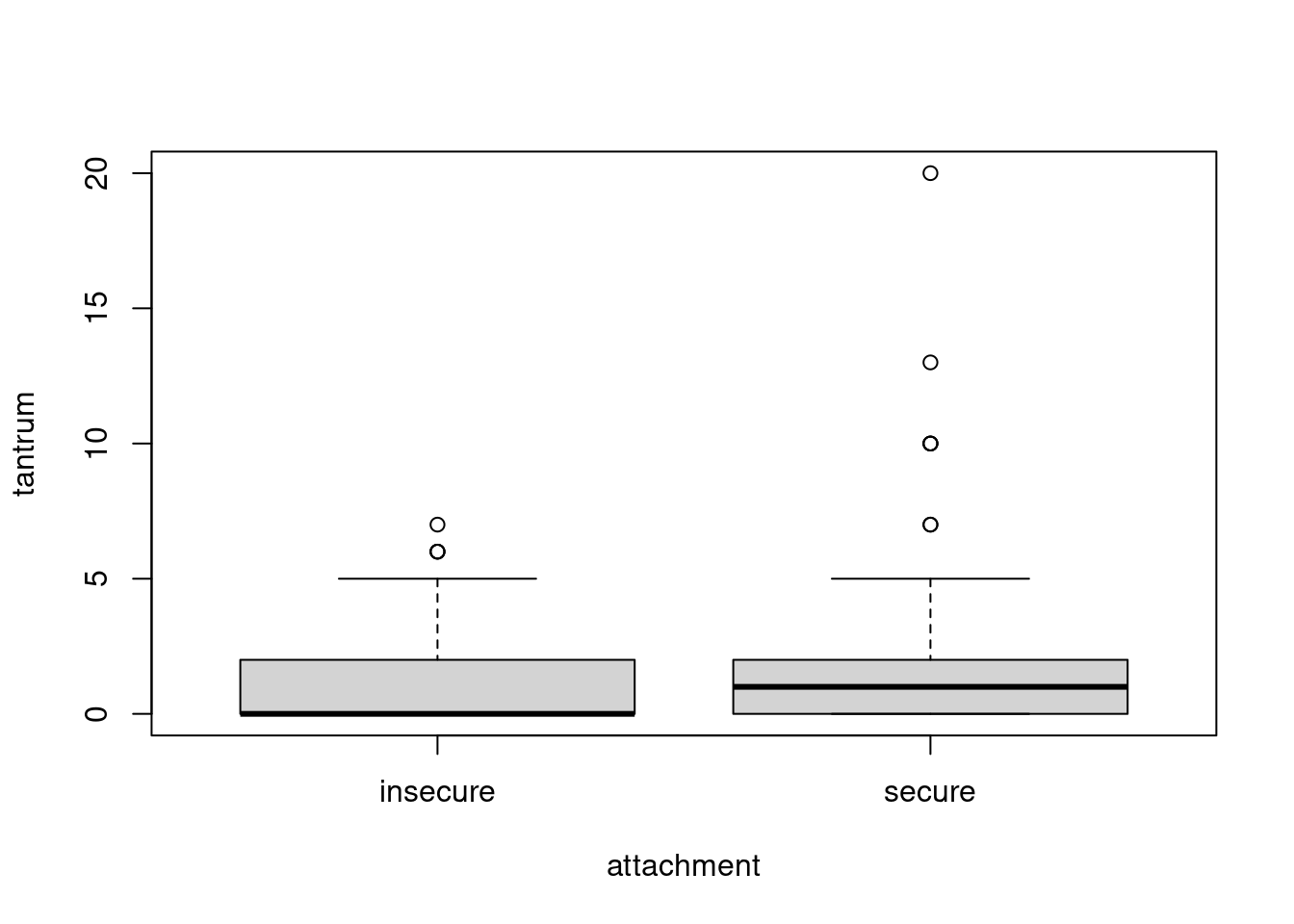

3. Model fitting with glm()

We can start by fitting our null model with the poisson() family:

fit0 <- glm(tantrum ~ 1, family = poisson(link = "log"), data = dat)

What is the intercept here?

Then we can fit a model with the attachment effect:

fit1 <- glm(tantrum ~ parent_se, family = poisson(link = "log"), data = dat)
summary(fit1)

Call:
glm(formula = tantrum ~ parent_se, family = poisson(link = "log"), 
    data = dat)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.1239  -1.8145  -0.8368   0.2666   7.3901  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)  0.02631    0.22966   0.115   0.9088  
parent_se    0.07870    0.03240   2.429   0.0151 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 421.11  on 117  degrees of freedom
Residual deviance: 415.05  on 116  degrees of freedom
AIC: 590.21

Number of Fisher Scoring iterations: 6

What about the overdispersion? What could be the reason?

Assuming that the attachment is the only variable that we have, we could estimate the degree of overdispersion:

sum(residuals(fit1, type = "pearson")^2)/fit1$df.residual
[1] 5.065601
performance::check_overdispersion(fit1)
# Overdispersion test

       dispersion ratio =   5.066
  Pearson's Chi-Squared = 587.610
                p-value = < 0.001
Overdispersion detected.

Let’s have a look also at the residual plot:

residualPlots(fit1)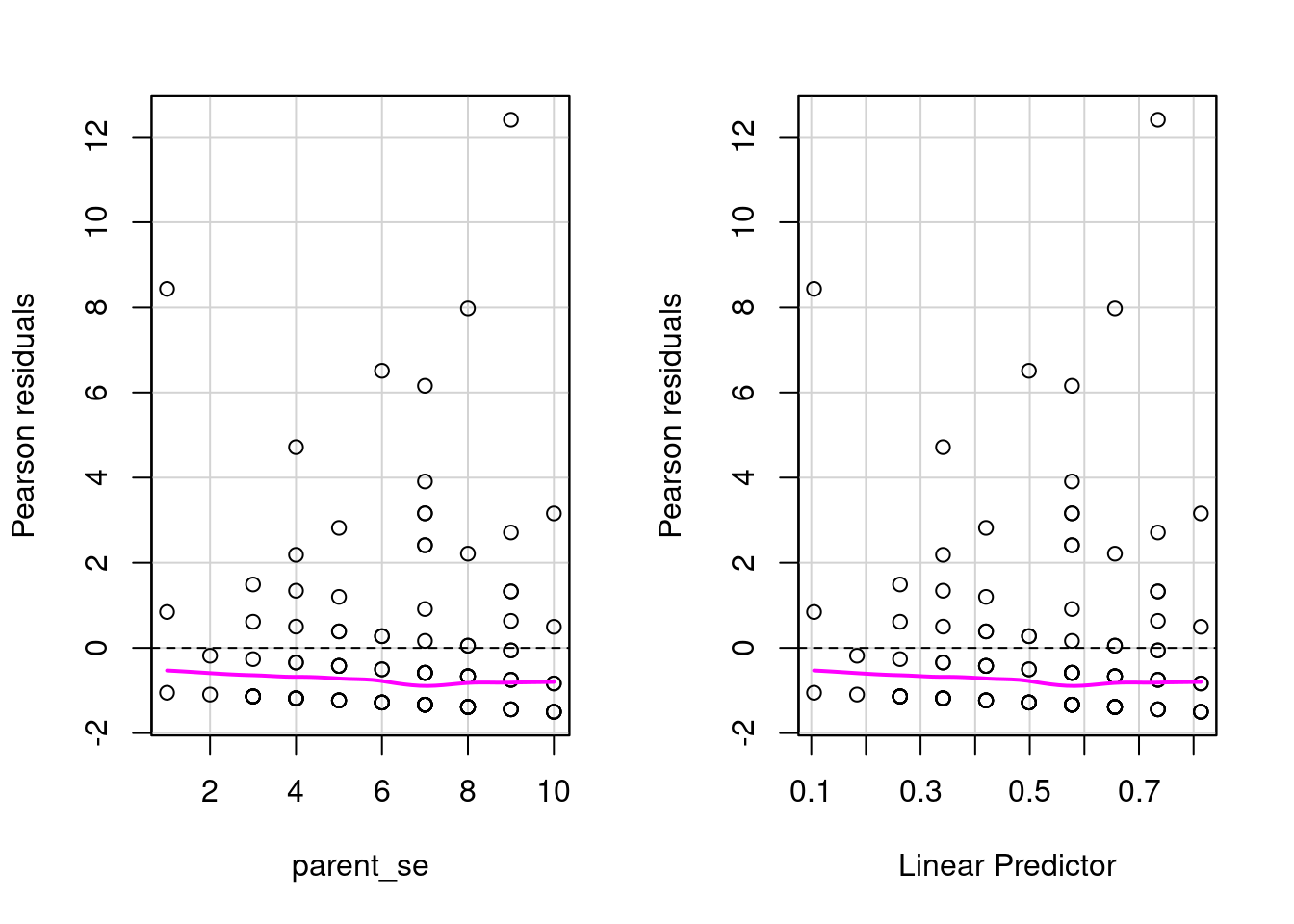

          Test stat Pr(>|Test stat|)  
parent_se    3.1933          0.07394 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

There is clear evidence of overdispersion. But we have several other variables so before using another model let’s fit everything:

fit_s <- glm(tantrum ~ attachment + temperament + parent_se + parent_skills, family = poisson(link = "log"), data = dat)
summary(fit_s)

Call:
glm(formula = tantrum ~ attachment + temperament + parent_se + 
    parent_skills, family = poisson(link = "log"), data = dat)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.9635  -1.0742  -0.6412   0.2012   7.7786  

Coefficients:
                 Estimate Std. Error z value Pr(>|z|)    
(Intercept)       3.19125    0.34888   9.147  < 2e-16 ***
attachmentsecure -0.05147    0.15964  -0.322    0.747    
temperamenteasy  -0.82435    0.14127  -5.835 5.36e-09 ***
parent_se        -0.01881    0.03605  -0.522    0.602    
parent_skills    -0.38883    0.03454 -11.257  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 421.11  on 117  degrees of freedom
Residual deviance: 218.91  on 113  degrees of freedom
AIC: 400.07

Number of Fisher Scoring iterations: 6

Let’s check again overdispersion and pearson residuals:

residualPlots(fit_s)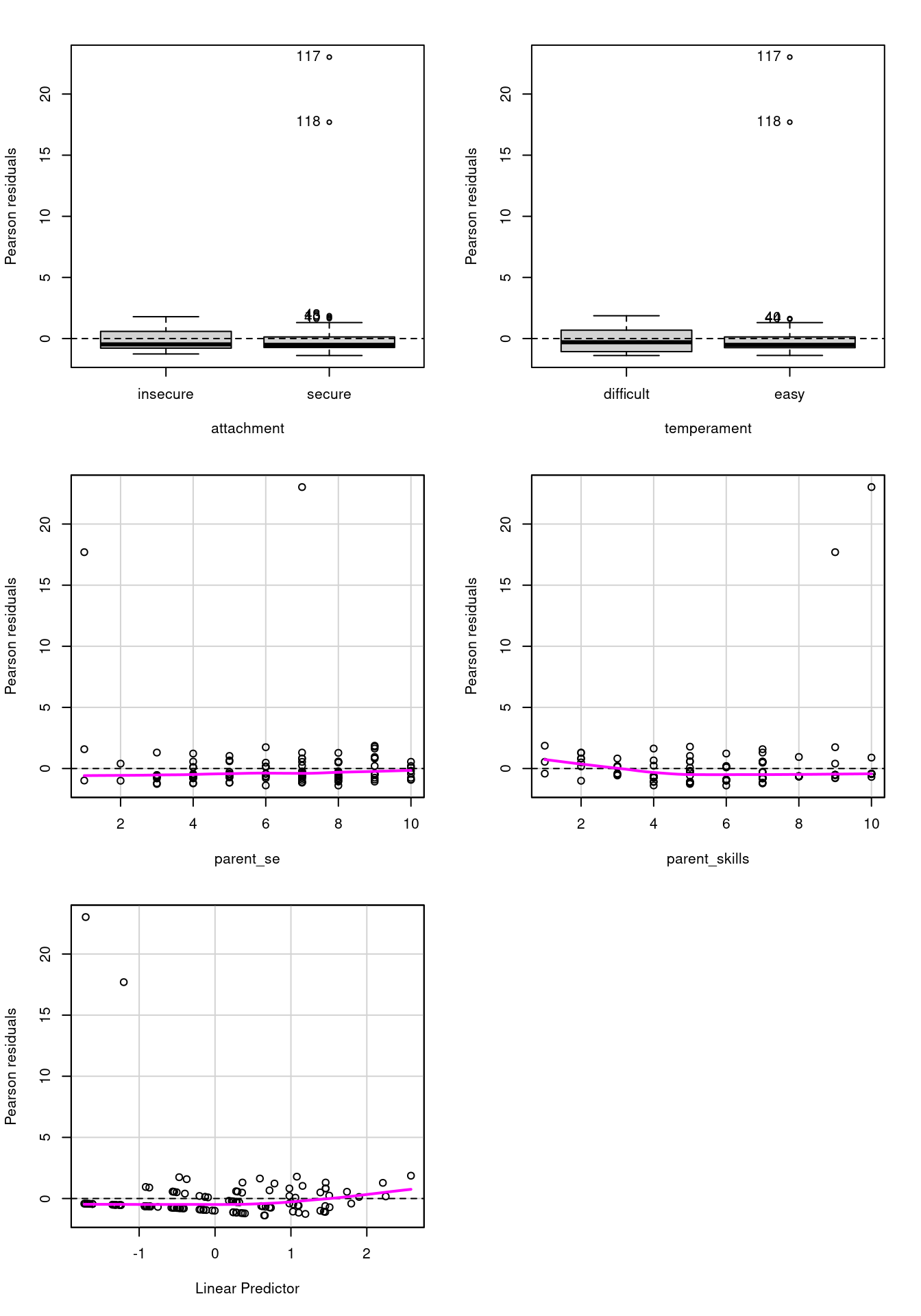

              Test stat Pr(>|Test stat|)    
attachment                                  
temperament                                 
parent_se        9.5838         0.001963 ** 
parent_skills   29.1366        6.745e-08 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The majority of the distribution seems ok, but there are some values with very high residuals and the overdispersion is still present:

sum(residuals(fit_s, type = "pearson")^2)/fit_s$df.residual
[1] 8.14082
performance::check_overdispersion(fit_s)
# Overdispersion test

       dispersion ratio =   8.141
  Pearson's Chi-Squared = 919.913
                p-value = < 0.001
Overdispersion detected.

4. Diagnostic

Another reason for overdispersion could be the presence of outliers and influential points. Let’s have a look at the Cook distances:

car::influenceIndexPlot(fit_s, vars = c("cook", "hat", "Studentized"))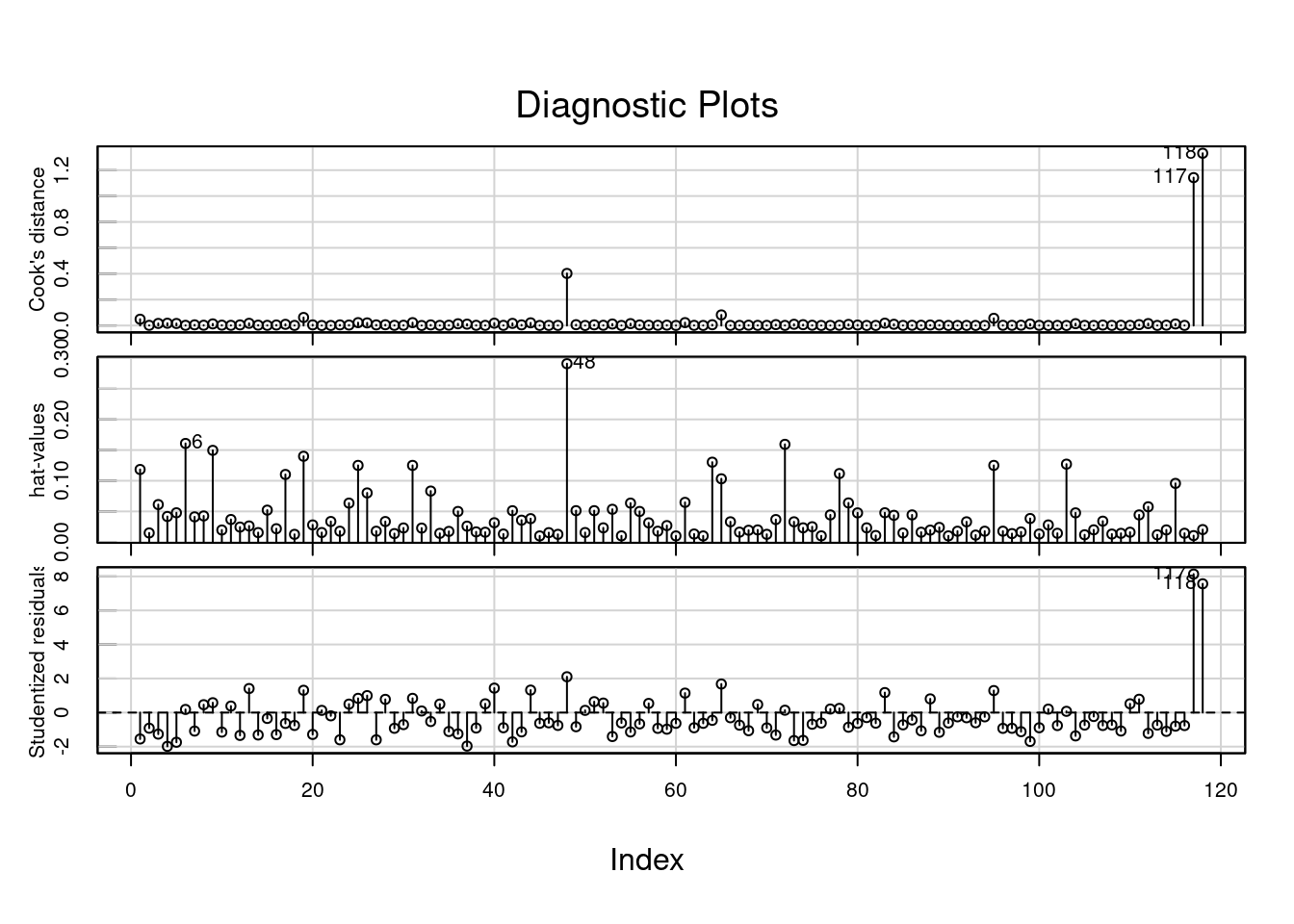

There are two values (117 and 118) with a very high cook distance and very high studentized residual. We can try to fit a model without these values and check what happens to the model:

dat_no_out <- dat[-c(117, 118), ]
fit_no_out <- glm(tantrum ~ attachment + temperament + parent_se + parent_skills, family = poisson(link = "log"), data = dat_no_out)
summary(fit_no_out)

Call:
glm(formula = tantrum ~ attachment + temperament + parent_se + 
    parent_skills, family = poisson(link = "log"), data = dat_no_out)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.6340  -0.7705  -0.4001   0.2804   2.1595  

Coefficients:
                 Estimate Std. Error z value Pr(>|z|)    
(Intercept)       3.72884    0.39403   9.463  < 2e-16 ***
attachmentsecure -0.41074    0.16838  -2.439   0.0147 *  
temperamenteasy  -1.08473    0.15090  -7.188 6.56e-13 ***
parent_se         0.01940    0.04055   0.478   0.6324    
parent_skills    -0.53074    0.04109 -12.915  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 382.413  on 115  degrees of freedom
Residual deviance:  84.882  on 111  degrees of freedom
AIC: 257.73

Number of Fisher Scoring iterations: 5

The model seems to be clearly improved, especially in terms of overdispersion:

sum(residuals(fit_no_out, type = "pearson")^2)/fit_no_out$df.residual
[1] 0.81442
performance::check_overdispersion(fit_no_out)
# Overdispersion test

       dispersion ratio =  0.814
  Pearson's Chi-Squared = 90.401
                p-value =  0.924
No overdispersion detected.

We can also compare the two models in terms of coefficients:

car::compareCoefs(fit_s, fit_no_out)
Calls:
1: glm(formula = tantrum ~ attachment + temperament + parent_se + 
  parent_skills, family = poisson(link = "log"), data = dat)
2: glm(formula = tantrum ~ attachment + temperament + parent_se + 
  parent_skills, family = poisson(link = "log"), data = dat_no_out)

                 Model 1 Model 2
(Intercept)        3.191   3.729
SE                 0.349   0.394
                                
attachmentsecure -0.0515 -0.4107
SE                0.1596  0.1684
                                
temperamenteasy   -0.824  -1.085
SE                 0.141   0.151
                                
parent_se        -0.0188  0.0194
SE                0.0360  0.0405
                                
parent_skills    -0.3888 -0.5307
SE                0.0345  0.0411

In fact, there are some coefficients with different values. We can check also the dfbeta plots:

dfbeta_plot(fit_s)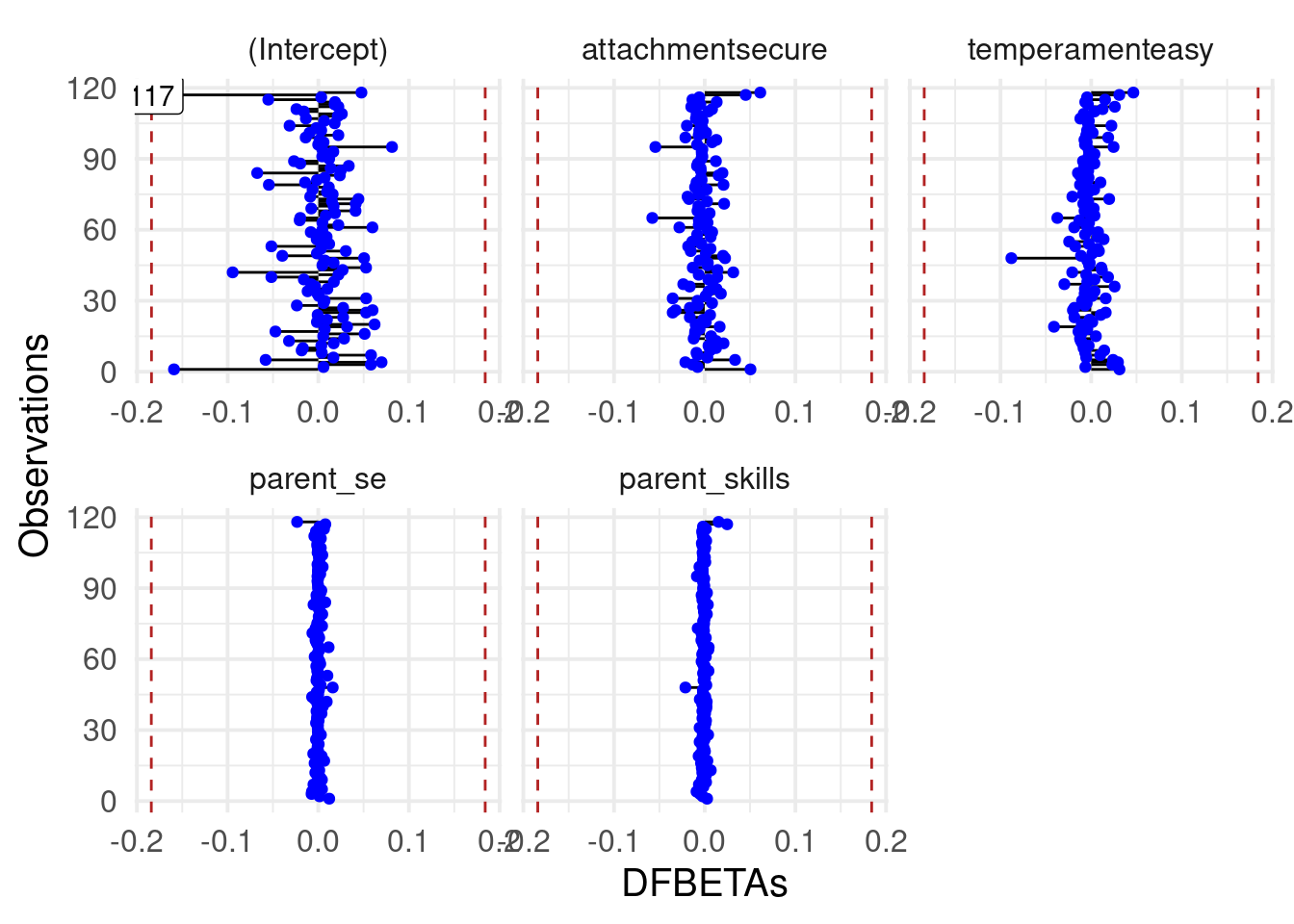

The previous observations seems to do not affect the estimated parameters but they impact the overall model fit, deviance and residuals.

Let’s have a look at residuals now:

car::residualPlot(fit_no_out)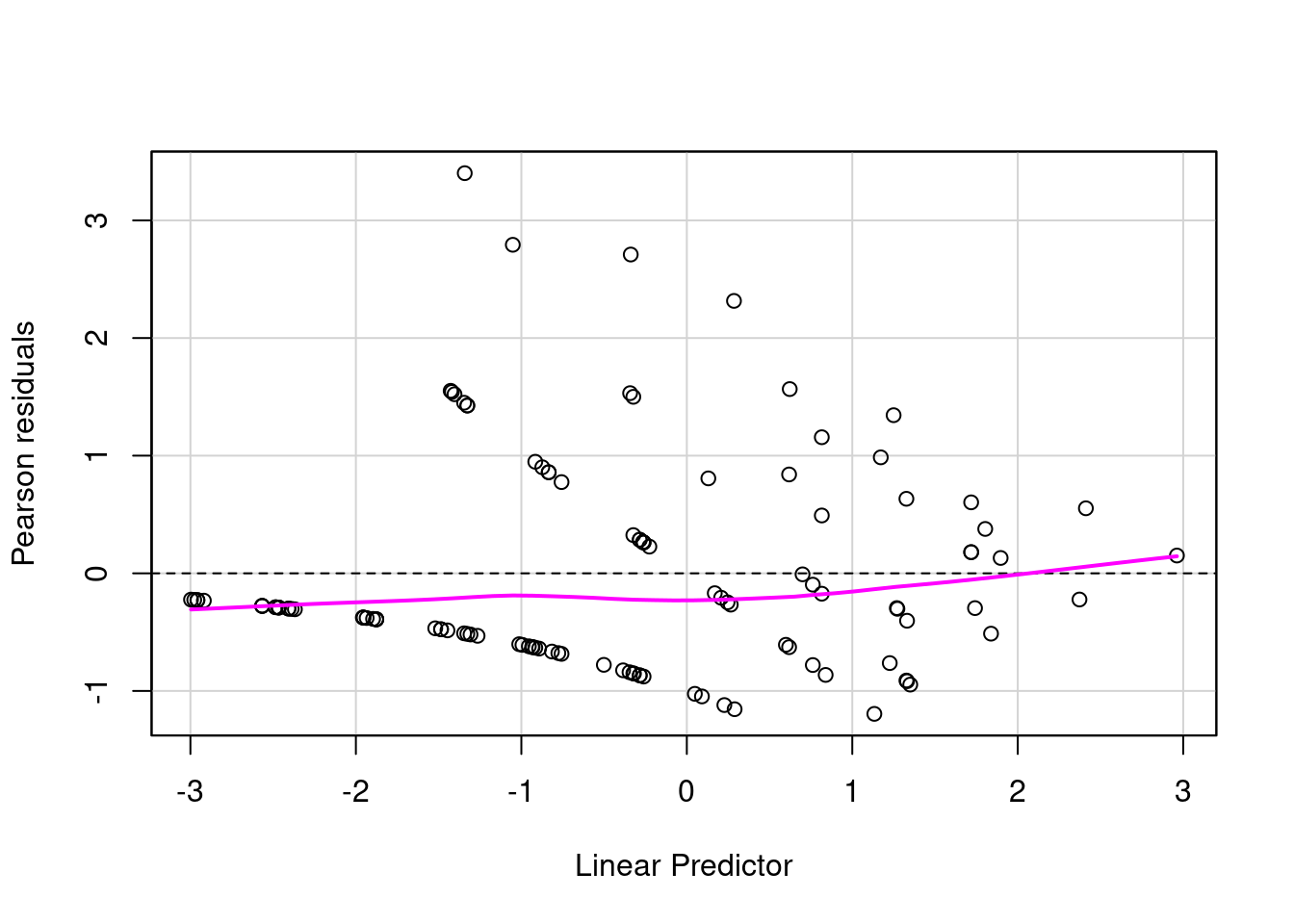

There is still some strange pattern but the majority of the distribution seems to be between -1 and 1.

5. Interpreting parameters

Before anything else, just plot the effects:

plot(allEffects(fit_no_out))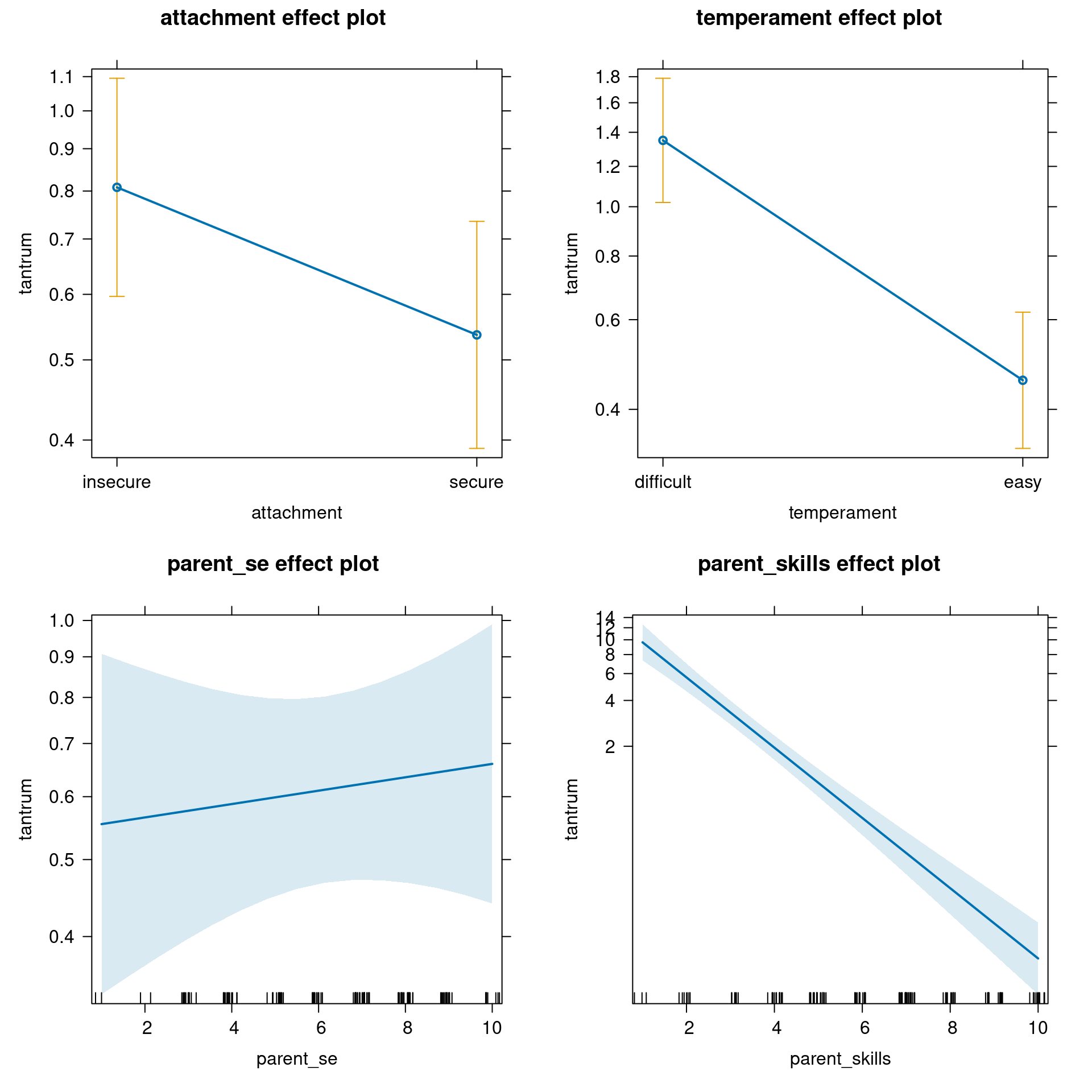

Now we can interpret model parameters:

summary(fit_no_out)

Call:
glm(formula = tantrum ~ attachment + temperament + parent_se + 
    parent_skills, family = poisson(link = "log"), data = dat_no_out)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.6340  -0.7705  -0.4001   0.2804   2.1595  

Coefficients:
                 Estimate Std. Error z value Pr(>|z|)    
(Intercept)       3.72884    0.39403   9.463  < 2e-16 ***
attachmentsecure -0.41074    0.16838  -2.439   0.0147 *  
temperamenteasy  -1.08473    0.15090  -7.188 6.56e-13 ***
parent_se         0.01940    0.04055   0.478   0.6324    
parent_skills    -0.53074    0.04109 -12.915  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 382.413  on 115  degrees of freedom
Residual deviance:  84.882  on 111  degrees of freedom
AIC: 257.73

Number of Fisher Scoring iterations: 5

The (Intercept) is the expected number of tantrums for “insecure”, “difficult” children where parent_skills are rated as 0 and parent self esteem is 0, thus 41.6307958. Similarly to the binomial lab, we could center the two numerical variables to have a more meaningful interpretation or we can use the predict function to obtain the values that we want.

predict(fit_no_out, newdata = data.frame(attachment = "insecure", 
                                         temperament = "difficult",
                                         parent_se = mean(dat$parent_se), 
                                         parent_skills = mean(dat$parent_skills)),
        type = "response") # same as exp(prediction)
       1 
1.719356

The attachmentsecure is the expected difference in log number of tantrums between secure - insecure attachment, controlling for other variables:

emmeans(fit_no_out, pairwise~attachment)
$emmeans
 attachment  emmean    SE  df asymp.LCL asymp.UCL
 insecure    0.0302 0.152 Inf    -0.268    0.3289
 secure     -0.3805 0.153 Inf    -0.679   -0.0816

Results are averaged over the levels of: temperament 
Results are given on the log (not the response) scale. 
Confidence level used: 0.95 

$contrasts
 contrast          estimate    SE  df z.ratio p.value
 insecure - secure    0.411 0.168 Inf   2.439  0.0147

Results are averaged over the levels of: temperament 
Results are given on the log (not the response) scale.

In terms of the response scale, we can intepret it as the multiplicative increase of the number of tantrums from secure to insecure attachment:

exp(coef(fit_no_out)["attachmentsecure"])
attachmentsecure 
       0.6631612

Moving from insecure from secure attachment, there is a decrease in the expected number of tantrums of 33.6838801 %.

The temperamenteasy can be interpreted in the same way:

emmeans(fit_no_out, pairwise~temperament)
$emmeans
 temperament emmean    SE  df asymp.LCL asymp.UCL
 difficult    0.367 0.143 Inf    0.0868     0.648
 easy        -0.717 0.152 Inf   -1.0161    -0.419

Results are averaged over the levels of: attachment 
Results are given on the log (not the response) scale. 
Confidence level used: 0.95 

$contrasts
 contrast         estimate    SE  df z.ratio p.value
 difficult - easy     1.08 0.151 Inf   7.188  <.0001

Results are averaged over the levels of: attachment 
Results are given on the log (not the response) scale. 
exp(coef(fit_no_out)["temperamenteasy"])
temperamenteasy 
      0.3379941

So there is a reduction of the 66.2005908 % by moving from difficult to easy temperament.

parent_se and parent_skills are interpreted similarly. The coefficient represent the increase/decrease in the log number of tantrums for a unit increase in the predictors.

exp(coef(fit_no_out)[4:5])
    parent_se parent_skills 
    1.0195878     0.5881722

So the number of tantrums seems to be unaffected by the parents self-esteem but as the parent skills increases there is a reduction in the number of tantrums.

6. Model selection

Let’s compare the model with and without the parent_se terms that appear to be not very useful:

fit_no_parent_se <- update(fit_no_out, . ~ . -parent_se)
summary(fit_no_parent_se)

Call:
glm(formula = tantrum ~ attachment + temperament + parent_skills, 
    family = poisson(link = "log"), data = dat_no_out)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.6052  -0.7389  -0.4018   0.2766   2.1726  

Coefficients:
                 Estimate Std. Error z value Pr(>|z|)    
(Intercept)       3.88096    0.23280  16.671  < 2e-16 ***
attachmentsecure -0.40422    0.16787  -2.408    0.016 *  
temperamenteasy  -1.08057    0.15080  -7.166 7.75e-13 ***
parent_skills    -0.53723    0.03905 -13.757  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 382.413  on 115  degrees of freedom
Residual deviance:  85.111  on 112  degrees of freedom
AIC: 255.96

Number of Fisher Scoring iterations: 5
anova(fit_no_parent_se, fit_no_out, test = "LRT")
Analysis of Deviance Table

Model 1: tantrum ~ attachment + temperament + parent_skills
Model 2: tantrum ~ attachment + temperament + parent_se + parent_skills
  Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1       112     85.111                     
2       111     84.882  1  0.22948   0.6319
drop1(fit_no_out, test = "LRT")
Single term deletions

Model:
tantrum ~ attachment + temperament + parent_se + parent_skills
              Df Deviance    AIC     LRT  Pr(>Chi)    
<none>             84.882 257.73                      
attachment     1   90.605 261.45   5.724   0.01674 *  
temperament    1  136.028 306.87  51.146 8.573e-13 ***
parent_se      1   85.111 255.96   0.229   0.63191    
parent_skills  1  304.711 475.56 219.829 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Or using the MuMIn::dredge() function:

fit_no_out <- update(fit_no_out, na.action = na.fail)
MuMIn::dredge(fit_no_out, rank = "AIC")
Fixed term is "(Intercept)"
Global model call: glm(formula = tantrum ~ attachment + temperament + parent_se + 
    parent_skills, family = poisson(link = "log"), data = dat_no_out, 
    na.action = na.fail)
---
Model selection table 
      (Int) att     prn_se prn_skl tmp df   logLik   AIC  delta weight
14  3.88100   +            -0.5372   +  4 -123.978 256.0   0.00  0.608
16  3.72900   +  0.0194000 -0.5307   +  5 -123.863 257.7   1.77  0.251
13  3.48300                -0.5133   +  3 -126.768 259.5   3.58  0.102
15  3.38600      0.0118300 -0.5090   +  4 -126.725 261.5   5.49  0.039
5   2.89700                -0.5160      2 -150.397 304.8  48.84  0.000
6   3.08300   +            -0.5235      3 -149.436 304.9  48.92  0.000
7   2.96600     -0.0082560 -0.5189      3 -150.376 306.8  50.80  0.000
8   3.08500   + -0.0002435 -0.5236      4 -149.436 306.9  50.92  0.000
11  0.16220      0.1467000           +  3 -234.197 474.4 218.44  0.000
12  0.06833   +  0.1469000           +  4 -233.778 475.6 219.60  0.000
9   1.13900                          +  2 -243.108 490.2 234.26  0.000
10  1.04200   +                      +  3 -242.642 491.3 235.33  0.000
3  -0.48580      0.1398000              2 -264.575 533.1 277.19  0.000
4  -0.52520   +  0.1395000              3 -264.498 535.0 279.04  0.000
1   0.45590                             1 -272.629 547.3 291.30  0.000
2   0.39690   +                         2 -272.475 549.0 292.99  0.000
Models ranked by AIC(x)

7. What about interactions?

We can also have a look at interactions, try by yourself to explore interactions between numerical (parent_skills and parent_se) and categorical (attachment and temperament) variables. I’m only interested in 1 continuous variable interacting with 1 categorical variable.

  • fit a separate model for each interaction
  • interpret the model parameters and the analysis of deviance table (car:: something :)) or using a model comparison (Likelihood Ratio Test) for testing the interaction
  • plot the model effects
  • comment the results