n <- 30
y <- rnorm(n, 50, 10)
mean(y)[1] 49.16878# sd(y) / sqrt(n)
B <- 1000
mm <- replicate(B, {
y <- rnorm(n, 50, 10)
mean(y)
})
hist(mm)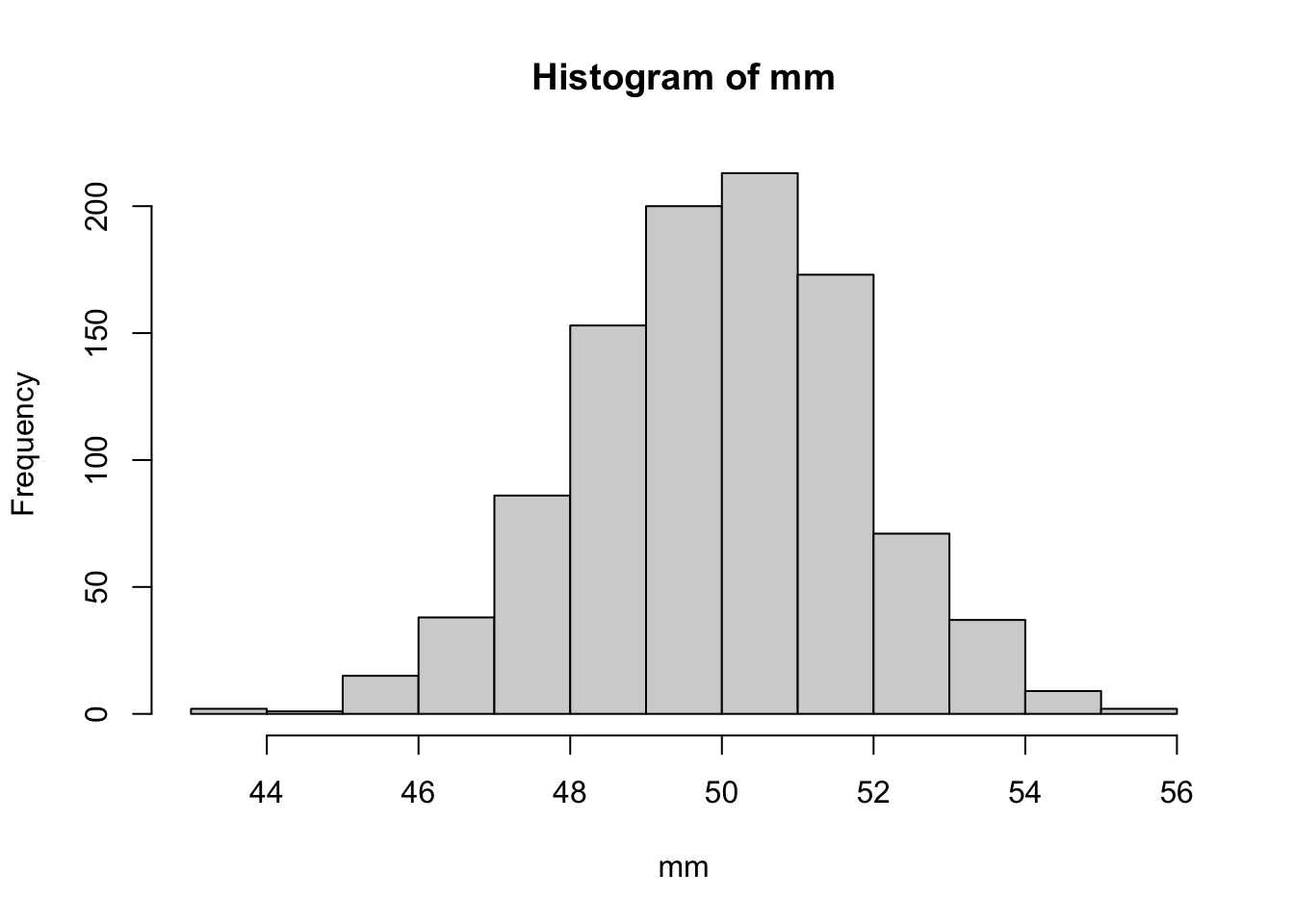
sd(mm)[1] 1.841226January 19, 2026
Estimating standard errors using Monte Carlo Simulations:
[1] 49.16878
[1] 1.841226Simulating and estimating power for a t-test
[1] 0.222
Two-sample t test power calculation
n = 30
d = 0.3
sig.level = 0.05
power = 0.2078518
alternative = two.sided
NOTE: n is number in *each* groupA more structured simulation:
sim_data <- function(n, d, s){
g1 <- rnorm(n, 0, s)
g2 <- rnorm(n, d, s)
dat <- data.frame(
y = c(g1, g2),
x = rep(0:1, each = n)
)
return(dat)
}
fit_model <- function(data){
t.test(y ~ x, data = data)$p.value
}
n <- c(10, 30, 50, 100)
res <- vector(mode = "list", length = length(n))
for(i in 1:length(n)){
res[[i]] <- replicate(B, {
dat <- sim_data(n[i], 0.5, 1)
fit_model(dat)
})
}
plot(n, sapply(res, function(x) mean(x <= 0.05)), type = "b")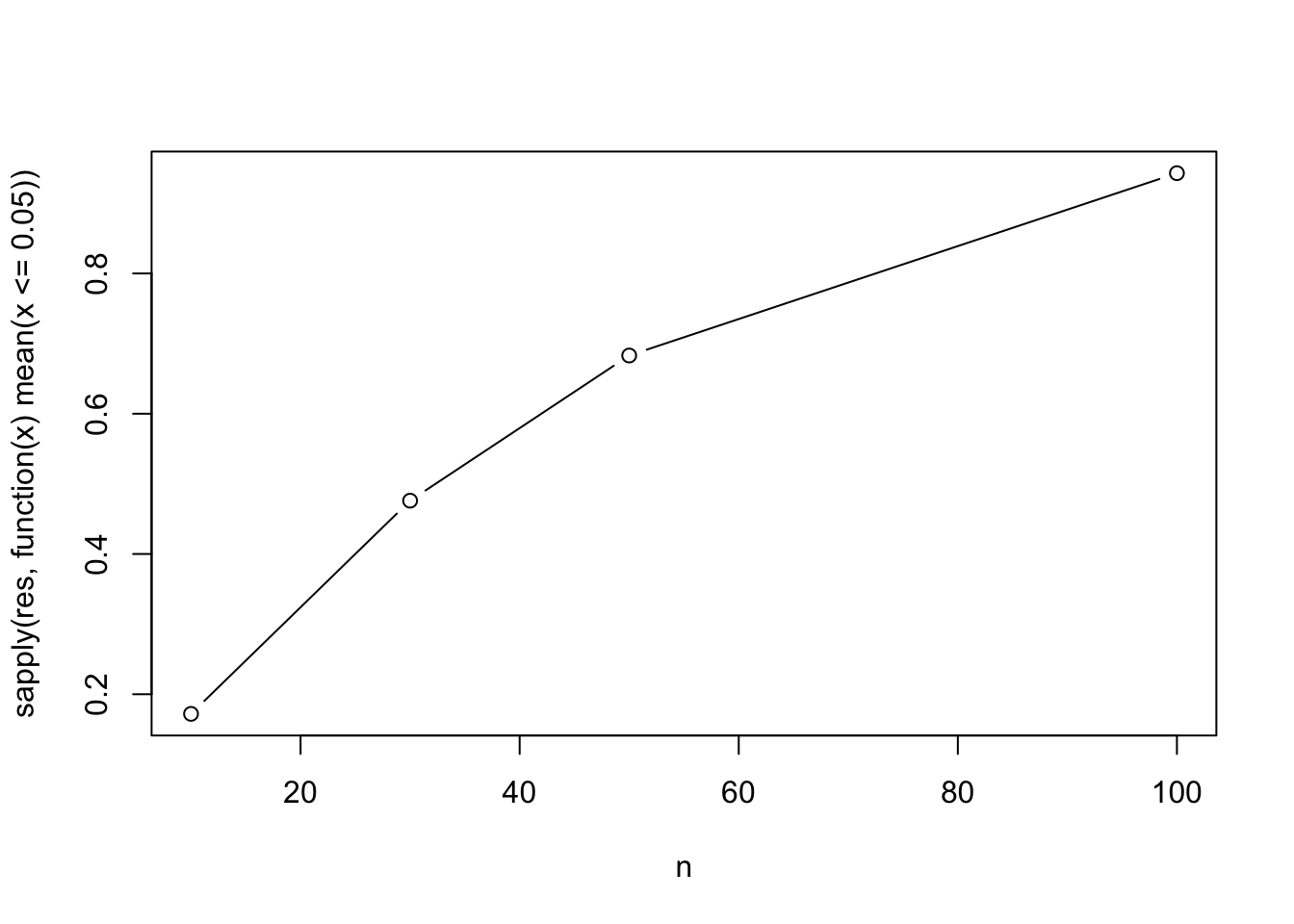
Simulating a GLM
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.26882170 0.031950948 71.009527 0.000000e+00
x 0.07013599 0.037234041 1.883652 5.961203e-02
age0 0.09516193 0.002476472 38.426412 4.940656e-323