2025-04-04

Author

Filippo Gambarota

In psicologia e neuroscienze alcuni esperimenti includono delle variabili che possono variare tra soggetti, nonostante siano manipolate sperimentalmente.

Ad esempio, in psicofisica gli stimoli vengono spesso adattati ai soggetti e quindi non tutti i soggetti sono sottoposti allo stesso tipo di stimolazione.

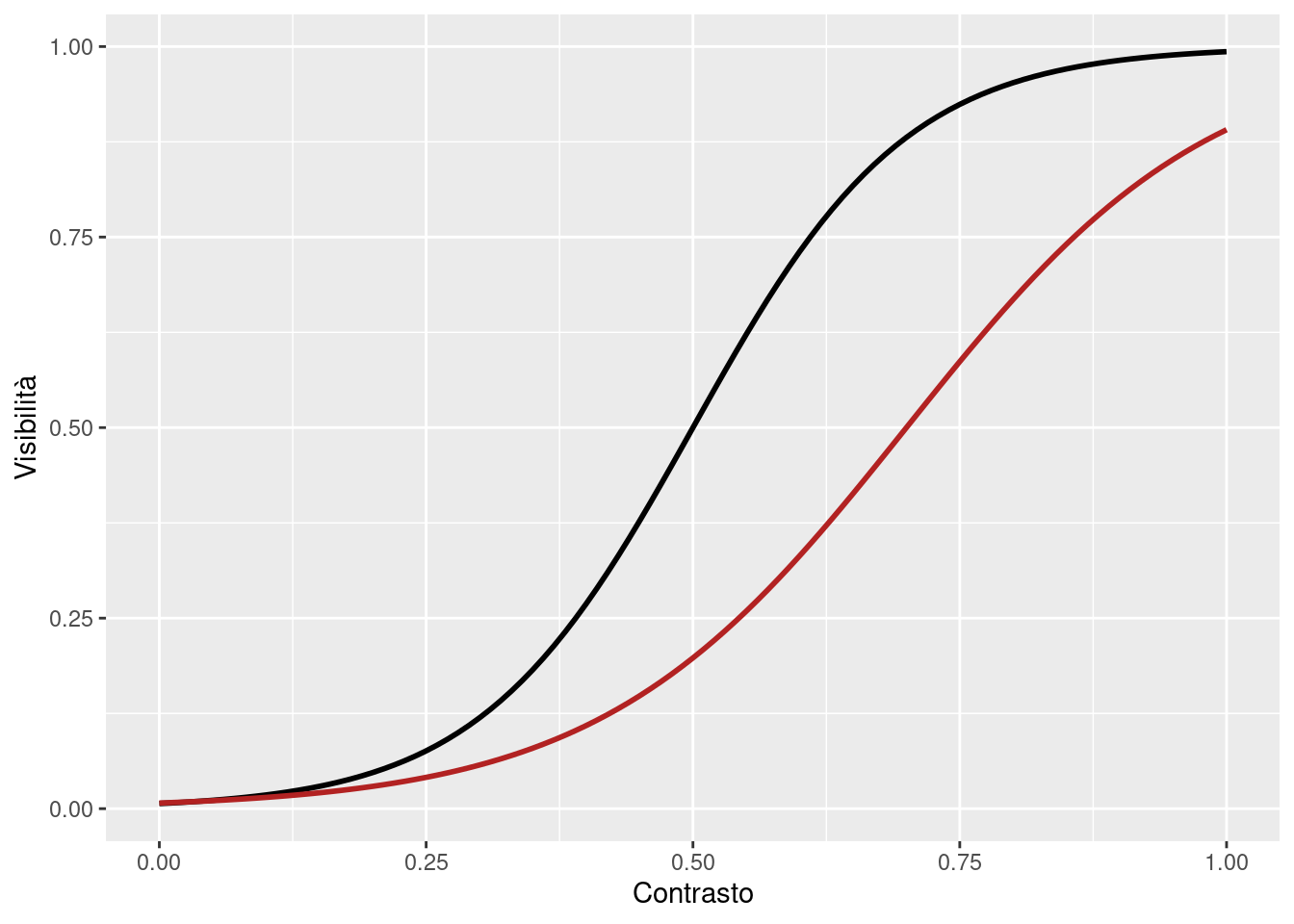
Ipotizziamo che siamo interessati a capire la sensibilità al contrasto (visibilità rispetto allo sfondo) di un gruppo di soggetti. A livello individuale possiamo ipotizzare che la relazione vera di due soggetti sia ad esempio:

Solitamente siamo interessati a stimare la soglia percettiva ed eventualmente la slope. La soglia percettiva è il livello di \(x\) (contrasto) necessario a ad avere una certa percentuale di visibilità (e.g., 50%).

Gli esperimenti possono essere tarati per adattare lo stimolo (contrasto) alle risposte permettendo di focalizzare i trial sulla parte della curva di interesse. Se proviamo a simulare due ipotetici esperimenti:

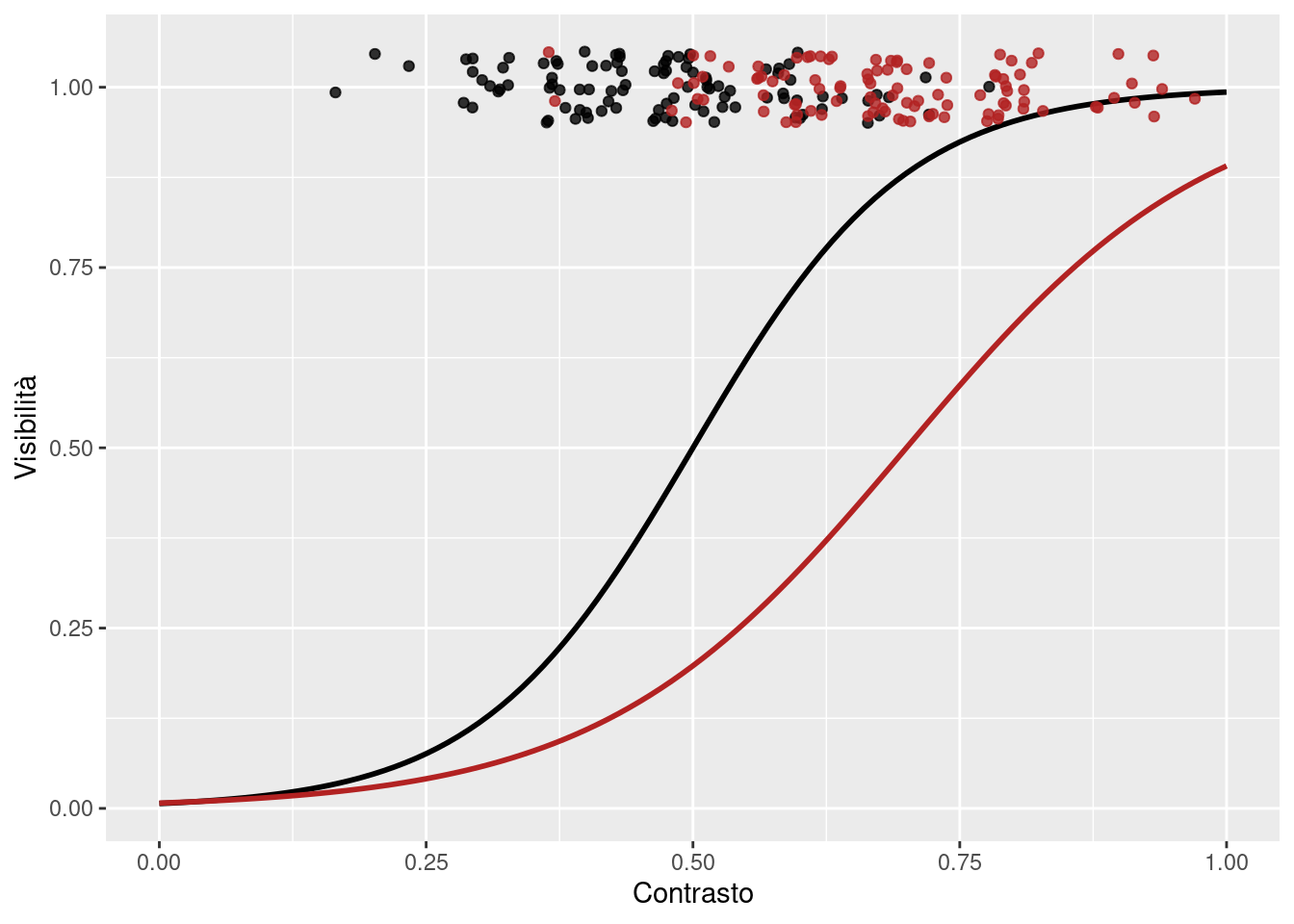
Ora carichiamo un dataset con un esperimento di questo tipo.

  id trial       x01 visibility
1  1     1 0.2069943          0
2  2     1 0.6339033          1
3  3     1 0.7137630          0
4  4     1 0.6853990          0
5  5     1 0.2117152          0
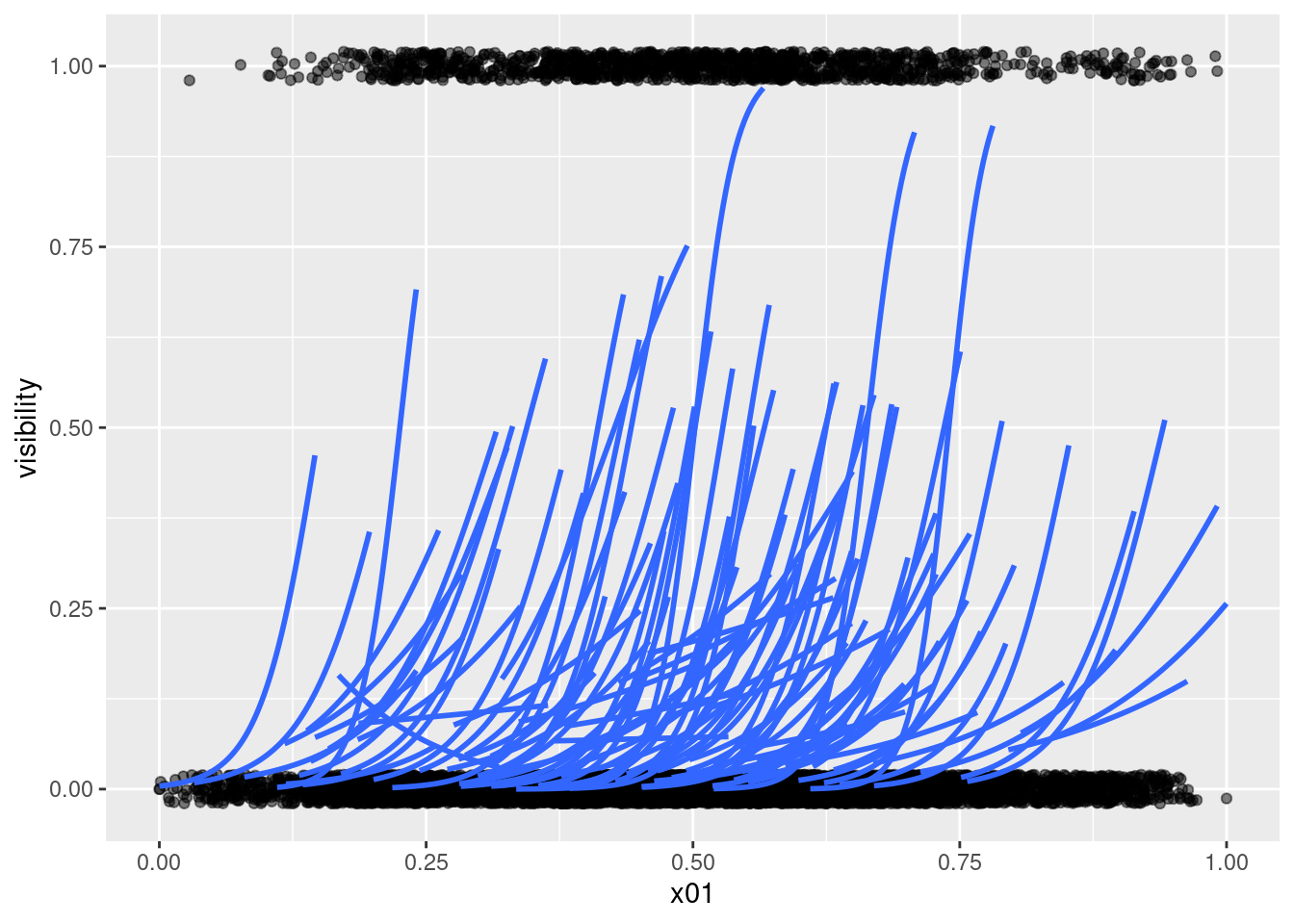
6  6     1 0.2450111          0

Possiamo anche vedere i pattern individuali:

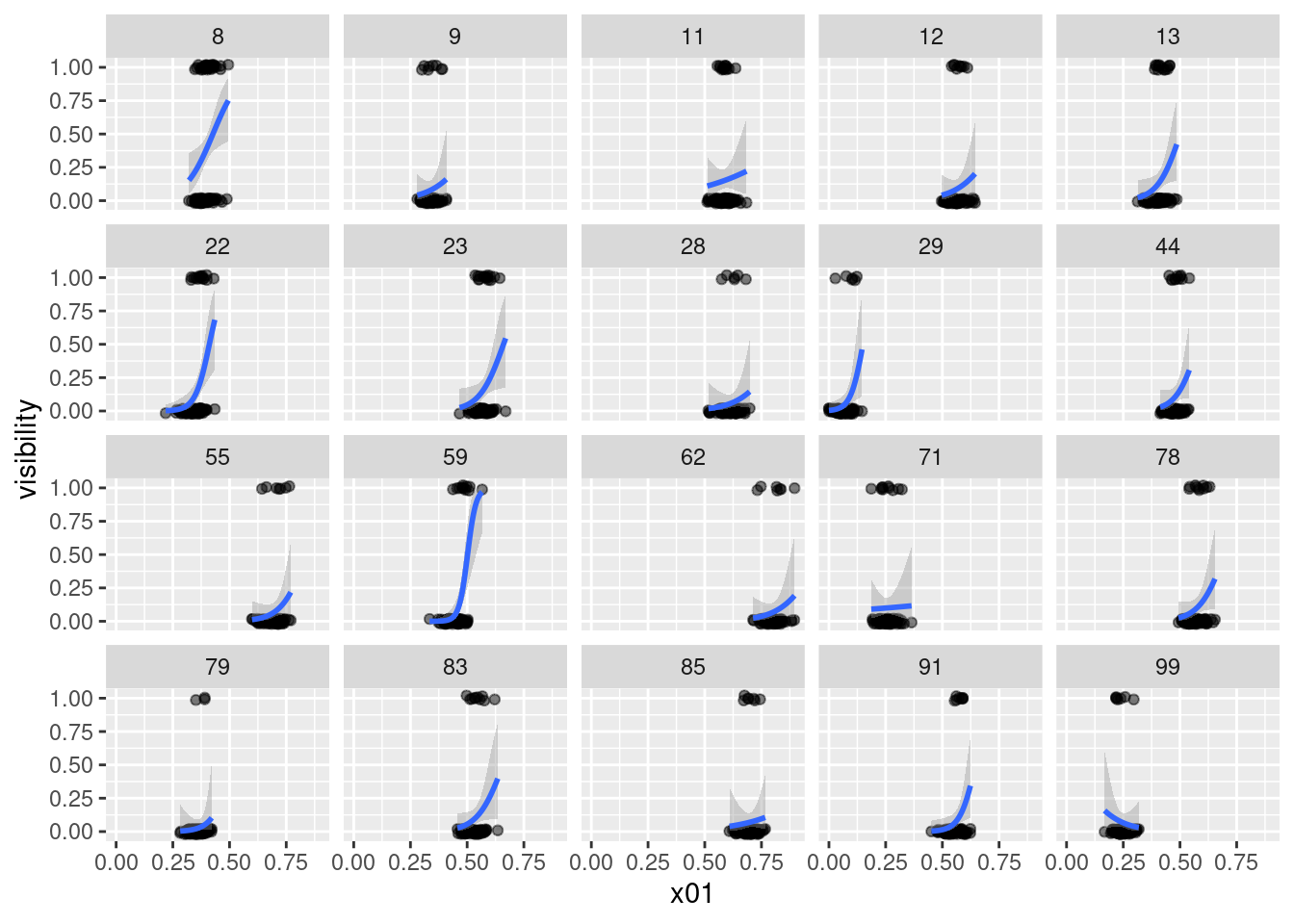
Fittiamo i nostri modelli per soggetto e vediamo il pattern di parametri:

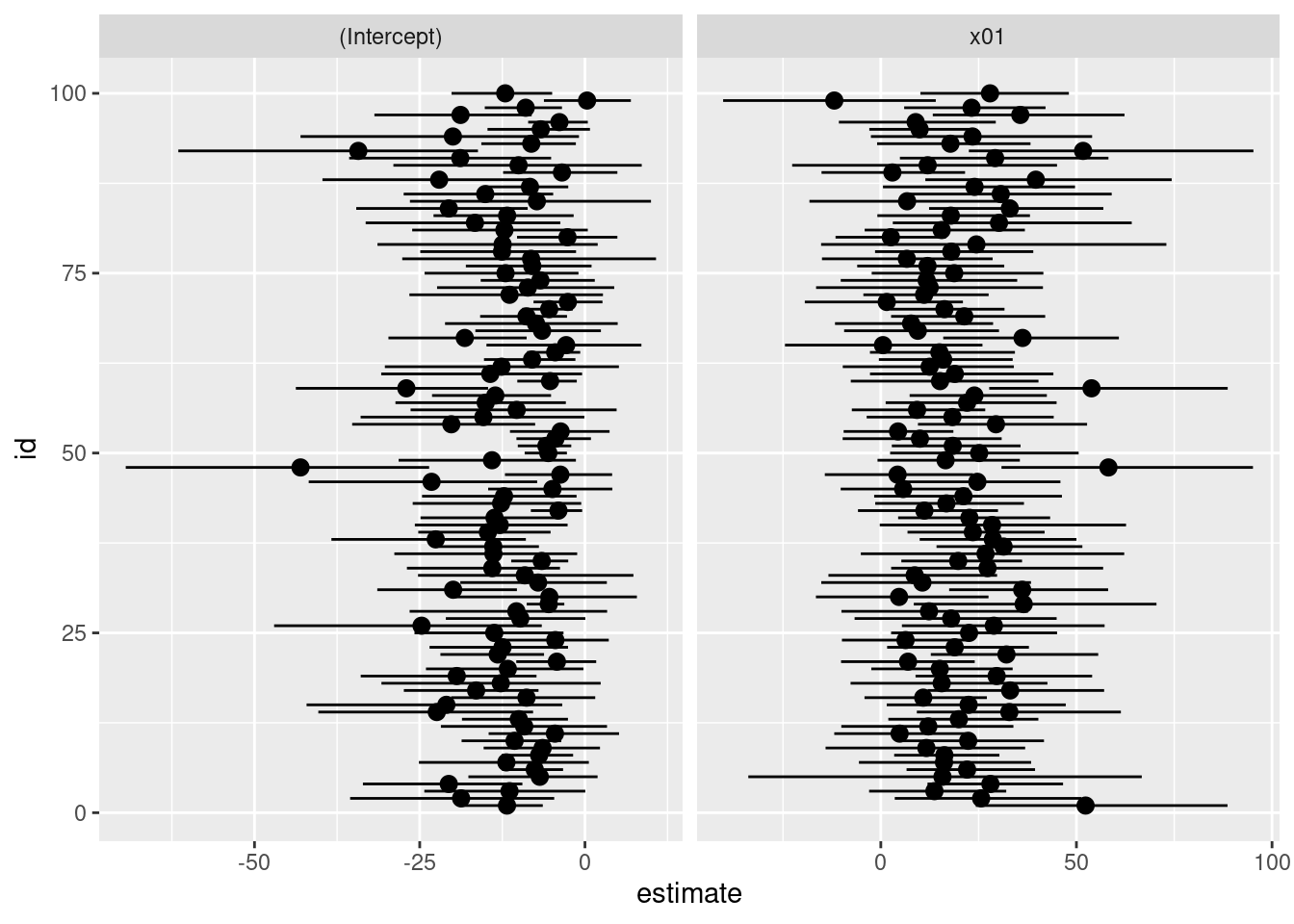
Perfetto, ora fittiamo il nostro modello:

library(lme4)
library(lmerTest)

fit <- glmer(visibility ~ x01 + (x01||id), data = dat, family = binomial(link = "logit"))
summary(fit)

Generalized linear mixed model fit by maximum likelihood (Laplace
  Approximation) [glmerMod]
 Family: binomial  ( logit )
Formula: visibility ~ x01 + (x01 || id)
   Data: dat

      AIC       BIC    logLik -2*log(L)  df.resid 
   7387.3    7416.2   -3689.7    7379.3      9996 

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-1.2114 -0.4091 -0.3261 -0.2499  8.6903 

Random effects:
 Groups Name        Variance Std.Dev.
 id     (Intercept) 2.217    1.489   
 id.1   x01         1.896    1.377   
Number of obs: 10000, groups:  id, 100

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)   -6.342      1.013  -6.258 3.91e-10 ***
x01            8.738      2.017   4.333 1.47e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
    (Intr)
x01 -0.984

library(ggeffects)
plot(ggeffect(fit))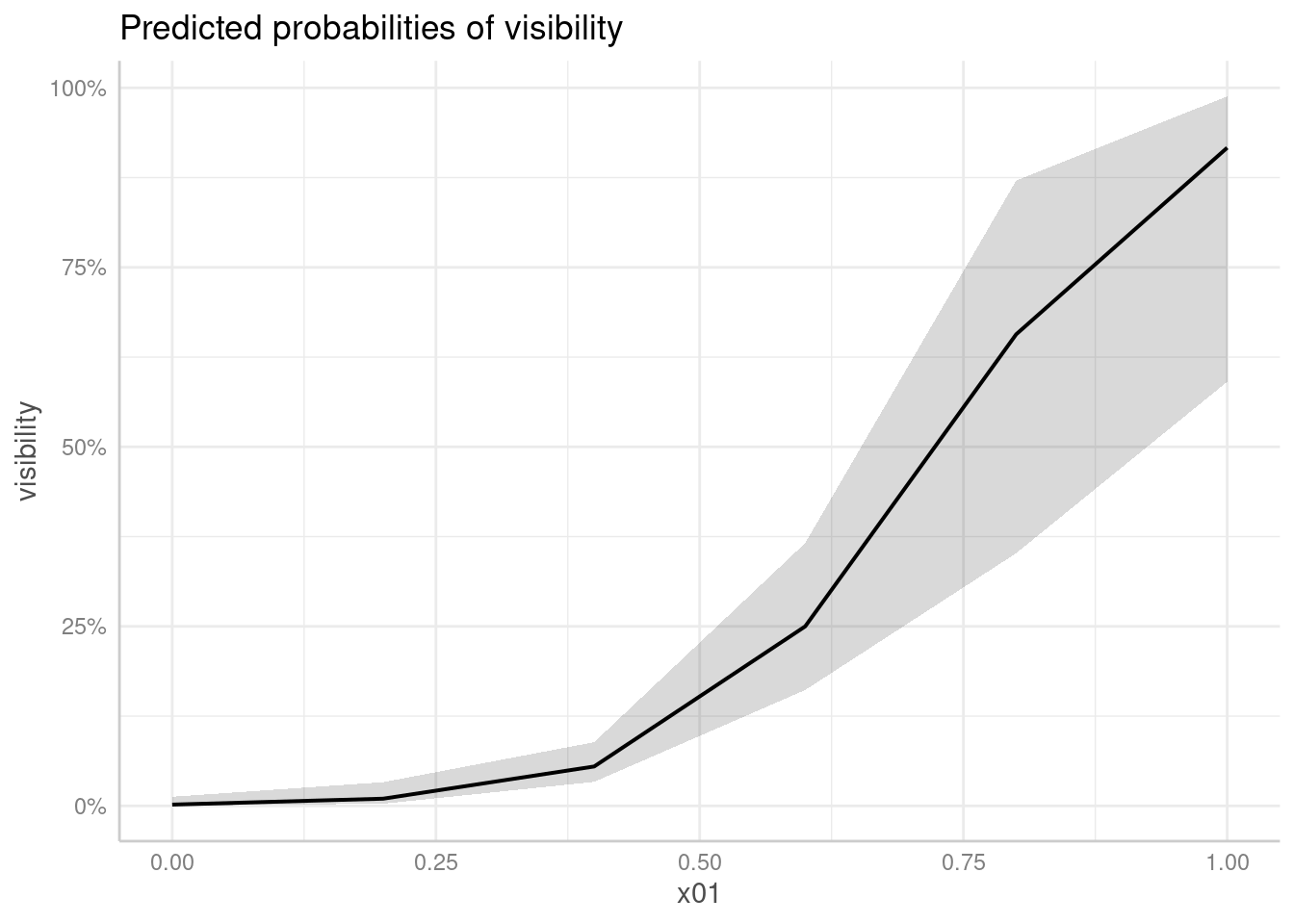

L’effetto fisso stimato dal modello è 8.74. Al netto dello shrinkage, questo è decisamente inferiore rispetto alla media delle slope stimate sui singoli soggetti. Quale potrebbe essere il motivo?

Il problema principale è che abbiamo un effetto del cluster (soggetti) sulla nostra variabile \(x\) (vi dice qualcosa il Simpson’s paradox?). Ogni soggetto ha il suo esperimento con un incremento chiaro (e consistente) della visibilità in funzione del contrasto MA i livelli di contrasto di ogni soggetto sono diversi uno dall’altro.

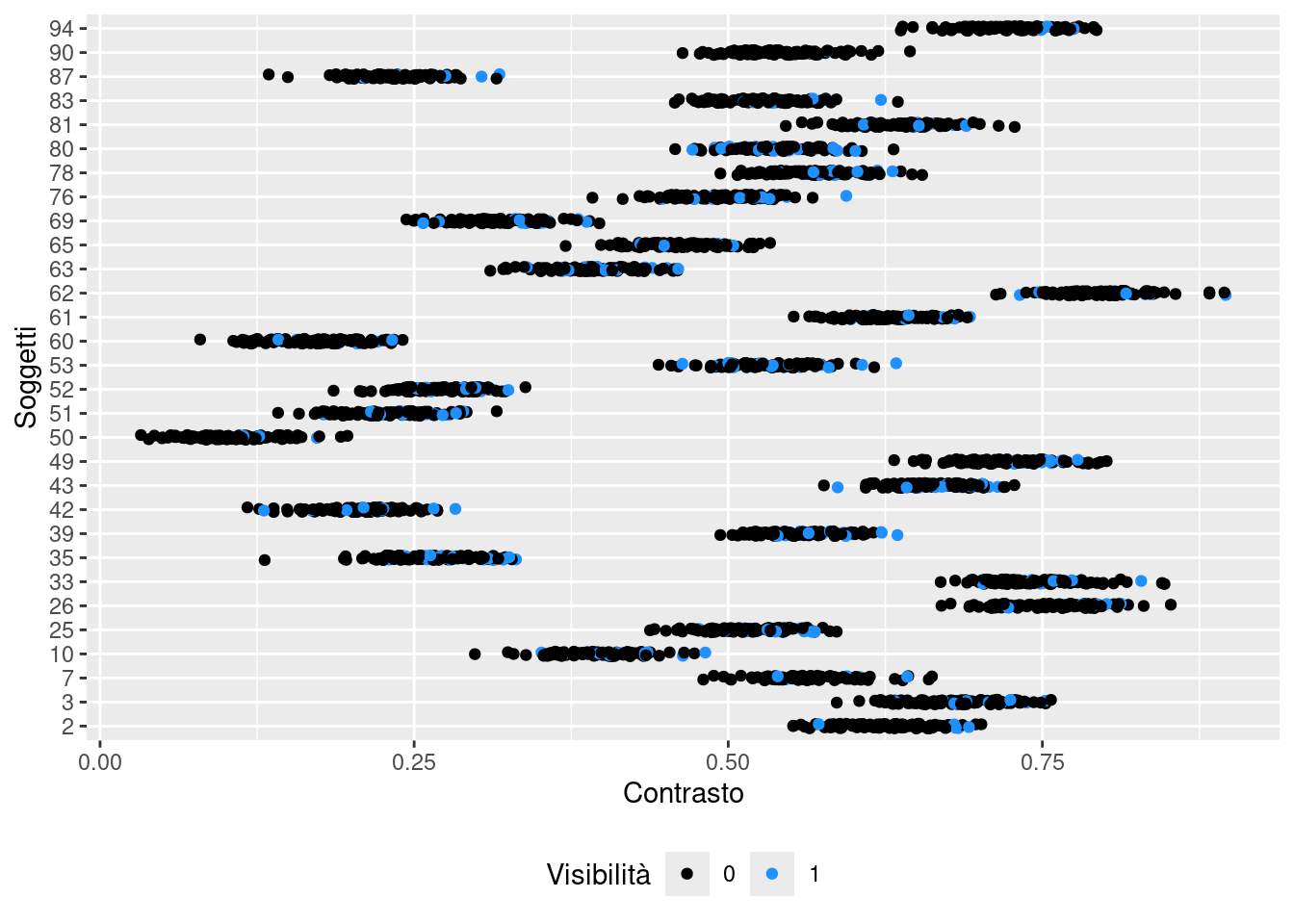
Quindi in realtà non stiamo stimando esattamente quello che vorremmo, ovvero l’effetto medio (e la sua variabilità) del contrasto in ogni soggetto. Idealmente dovremmo calcolarlo su ogni soggetto e poi fare la media.

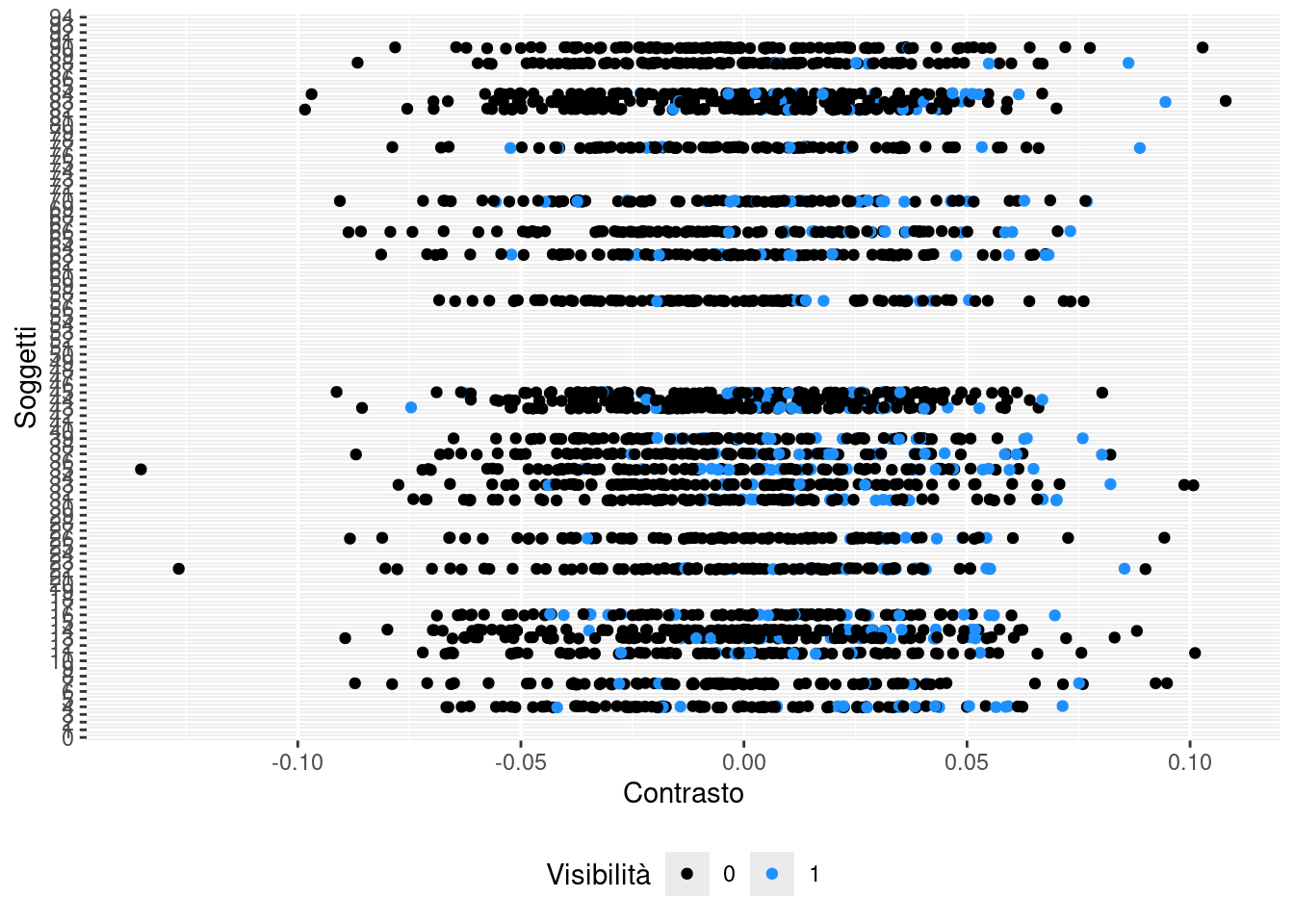
Per fare questo è necessario trasformare la \(x\), centrando i valori di contrasto sulla media di ogni soggetto.

cmc <- function(x, cluster){
  x - cm(x, cluster)
}
cm <- function(x, cluster){
    cmm <- tapply(x, cluster, mean)
    cmn <- tapply(x, cluster, length) 
    cmm[as.character(cluster)]
}

dat_ex$x01_cmc <- cmc(dat_ex$x01, dat_ex$id)
fit_cmc <- glmer(visibility ~ x01_cmc + (x01_cmc||id), data = dat_ex, family = binomial(link = "logit"))
summary(fit_cmc)

Generalized linear mixed model fit by maximum likelihood (Laplace
  Approximation) [glmerMod]
 Family: binomial  ( logit )
Formula: visibility ~ x01_cmc + (x01_cmc || id)
   Data: dat_ex

      AIC       BIC    logLik -2*log(L)  df.resid 
   7081.7    7110.5   -3536.8    7073.7      9996 

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-1.5490 -0.4042 -0.3101 -0.2293  6.2565 

Random effects:
 Groups Name        Variance Std.Dev.
 id     (Intercept) 0.2294   0.4789  
 id.1   x01_cmc     7.6120   2.7590  
Number of obs: 10000, groups:  id, 100

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -2.15515    0.05998  -35.93   <2e-16 ***
x01_cmc     18.17924    1.03817   17.51   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
        (Intr)
x01_cmc -0.224

Se erroneamente (qualche volta viene fatto), decidiamo di aggregare i dati a livello del soggetto. Possiamo nel migliore dei casi attenuare o distorcere la stima oppure stimare un pattern anche opposto.

dat_agg <- dat_ex |> 
    group_by(id) |> 
    summarise(p = mean(visibility),
              n = n(),
              x01 = mean(x01))
head(dat_agg)

# A tibble: 6 × 4
     id     p     n   x01
  <int> <dbl> <int> <dbl>
1     1  0.11   100 0.171
2     2  0.08   100 0.623
3     3  0.12   100 0.680
4     4  0.21   100 0.679
5     5  0.02   100 0.180
6     6  0.17   100 0.264

fit_agg <- glmer(p ~ x01 + (1|id), data = dat_agg, weights = n, family = binomial(link = "logit"))
summary(fit_agg)

Generalized linear mixed model fit by maximum likelihood (Laplace
  Approximation) [glmerMod]
 Family: binomial  ( logit )
Formula: p ~ x01 + (1 | id)
   Data: dat_agg
Weights: n

      AIC       BIC    logLik -2*log(L)  df.resid 
    633.0     640.8    -313.5     627.0        97 

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-1.62242 -0.44308  0.02905  0.35862  1.33912 

Random effects:
 Groups Name        Variance Std.Dev.
 id     (Intercept) 0.2064   0.4543  
Number of obs: 100, groups:  id, 100

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -1.9989     0.1605 -12.455   <2e-16 ***
x01          -0.0477     0.3052  -0.156    0.876    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
    (Intr)
x01 -0.938