2025-05-09

Esercizi

Meta-analisi

Dal pacchetto psymetadata provate a scegliere un dataset ed analizzarlo e applicare i modelli che abbiamo visto sia per stimare gli effetti che publication bias. Scegliete il dataset che volete, questi sono un paio di consigliati.

# install.packages("psymetadata")

library(psymetadata)

data("gnambs2020")
data("spaniol2020")

Mixed-effects models

Il dataset data/rt.rds contiene un esperimento di tempi di reazione (colonna rt). L’ipotesi principale è una differenza in funzione della congruenza dello stimolo (congruence). Scegliere il modello più adatto, intepretare gli effetti, etc.

• c’è anche una colonna con la data dell’esperimento. Vedere se c’è un impatto nell’effetto e nei tempi di reazione in funzione al periodo della giornata (mattina < 12:00pm, pomeriggio 12-17, sera dopo le 17:00).
• vedere relazione tra accuratezza (correct) e tempi di reazione

dat <- readRDS(here::here("data", "rt.rds"))
head(dat)

  id          local_date congruence    rt correct trial_number
1  1 16/06/2022 09:18:11          c 809.6       1            1
2  1 16/06/2022 09:18:12          c 484.8       1            2
3  1 16/06/2022 09:18:13          i 386.3       1            3
4  1 16/06/2022 09:18:15          c 676.3       1            4
5  1 16/06/2022 09:18:16          i 542.0       1            5
6  1 16/06/2022 09:18:18          c 924.7       1            6

Il dataset lo potete trovare su Github o scaricarlo qui.

Permutazioni

Abbiamo visto velocemente come implementare un test di permutazione per la differenza tra due gruppi.

N <- 100
x <- rep(0:1, each = N/2) # dummy
y <- 0.5 * x + rnorm(N, 0, 1) # 0.5 effect size + random noise

B <- 5000 # numero di permutazioni

tp <- rep(NA, B) # preallochiamo il vettore
tp[1] <- t.test(y ~ x)$statistic # prima permutazione i dati osservati

for(i in 2:B){
    xp <- sample(x)
    tp[i] <- t.test(y ~ xp)$statistic
}

hist(tp)
abline(v = tp[1])
points(tp[1], 0, pch = 19, cex = 2, col = "firebrick")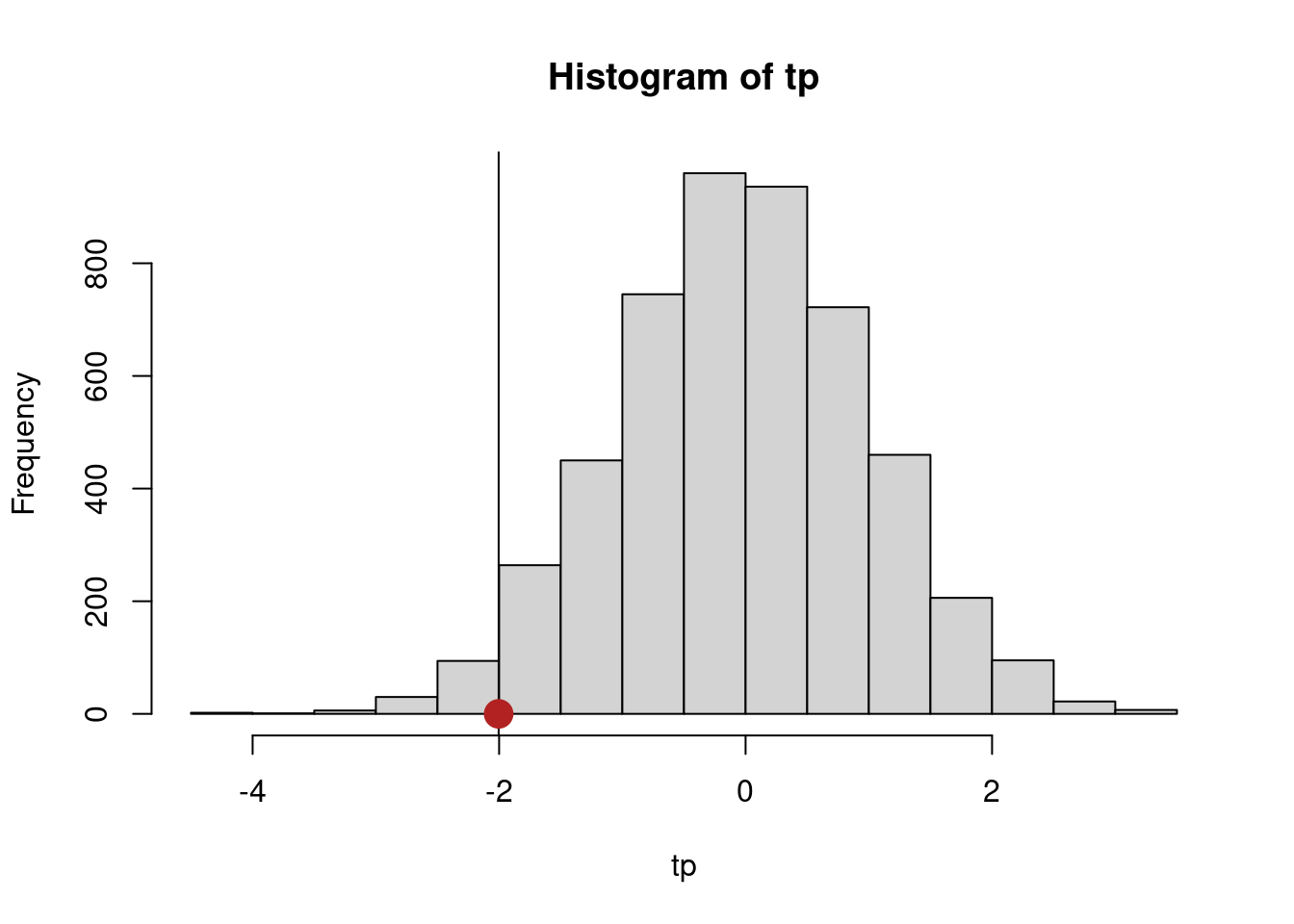

# p-value with permutations
mean(abs(tp) >= abs(tp[1]))

[1] 0.0512

Per un test ad un campione, è necessario permutare il segno:

y <- rnorm(N, 0.3, 1)
tp <- rep(NA, B)
tp[1] <- t.test(y, mu = 0)$statistic

for(i in 2:B){
    s <- sample(c(-1, 1), N, replace = TRUE)
    yp <- y * s
    tp[i] <- t.test(yp, mu = 0)$statistic
}

hist(tp)
abline(v = tp[1])
points(tp[1], 0, pch = 19, cex = 2, col = "firebrick")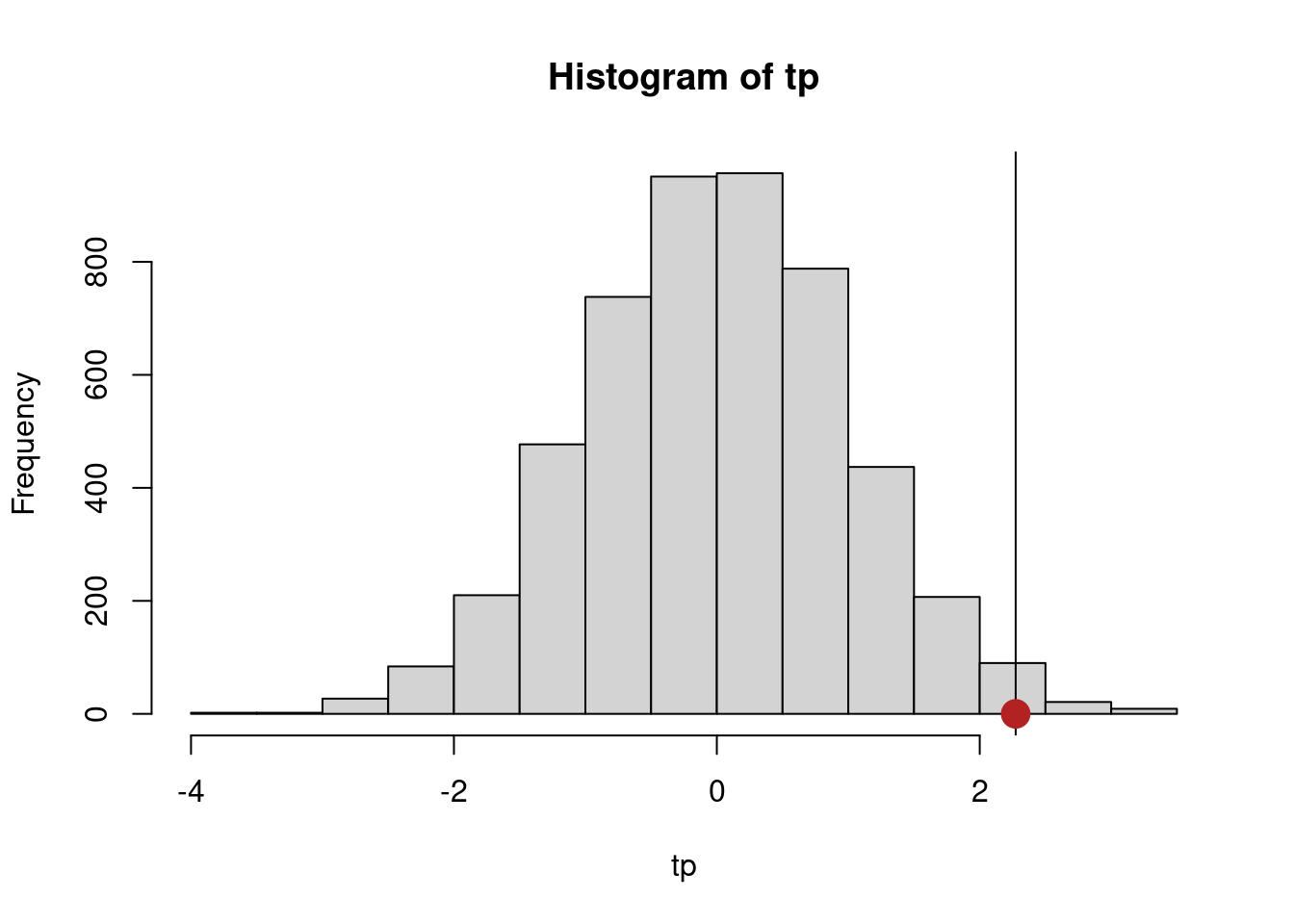

# p-value with permutations
mean(abs(tp) >= abs(tp[1]))

[1] 0.0268